PRODUCER-CONSUMER
In this simple example program, Producer-Consumer Pattern has been used. CopulaQueue class is nothing more, than just a wrapper for thread-safe ConcurrentQueue data structure. More specifically, the part of the program which actually creates all correlated random numbers into CopulaQueue, is the Producer. In the program, concrete CopulaEngine implementation class takes concrete RandomGenerator implementation class and correlation matrix as its input parameters. Concrete CopulaEngine implementation class then creates correlated random numbers and uses C# Event for sending created random number matrices to CopulaQueue. Another part of the program is the Consumer. Here, I have created a simple consumer class which simply prints created random numbers to console. Consumer class also uses C# Event for Dequeueing random number matrices from CopulaQueue. Needless to say, this (Consumer) is the part of our program, where we should be utilizing all correlated random numbers created by the Producer.
On design side, this program is closely following the program presented in the blog posting referred above. Again, the beef in this design is on its flexibility to allow any new implementations for Random generator and Copula model. Moreover, our example program is using C# Framework Parallel class method Parallel.ForEach, found under System.Threading.Tasks namespace. Example program creates four producers and consumers (both into List data structure) and using multi-threading (Parallel.ForEach) when processing correlated random numbers into/from CopulaQueue.
C# PROGRAM
In order to make everything as smooth as possible for the program replication, I have been writing all required classes in the same file. Just create a new console application and copy-paste the following program into a new .cs file.using System; using System.Diagnostics; using System.Linq; using System.Collections.Generic; using System.Threading.Tasks; using System.Collections.Concurrent; // namespace MultithreadingCopula { // public delegate methods needed for sending and receiving matrix data public delegate void MatrixSender(double[,] matrix); public delegate double[,] MatrixReceiver(); // ******************************************************************** // // the main program class Program { static void Main(string[] args) { try { // start timer Stopwatch timer = new Stopwatch(); timer.Start(); // // PRODUCER PART // create copula implementation, correlation matrix data and list of copula engines CopulaQueue copulaQueue = new CopulaQueue(); double[,] correlationMatrix = createCorrelationMatrix(); List<CopulaEngine> engines = new List<CopulaEngine>(); int nEngines = 4; int nRandomArrays = 25000; for (int i = 0; i < nEngines; i++) { engines.Add(new GaussianCopula(nRandomArrays, correlationMatrix, new CSharpRandom())); ((GaussianCopula)engines[i]).SendMatrix += copulaQueue.Enqueue; } // process all copula engines (producers) in parallel Parallel.ForEach(engines, engine => engine.Process()); // // CONSUMER PART // create list of consumers List<Consumer> consumers = new List<Consumer>(); int nConsumers = nEngines; for (int i = 0; i < nConsumers; i++) { consumers.Add(new Consumer(nRandomArrays, "consumer_" + (i + 1).ToString())); consumers[i].ReceiveMatrix += copulaQueue.Dequeue; } // process all consumers in parallel Parallel.ForEach(consumers, consumer => consumer.Process()); // // stop timer, print elapsed time to console timer.Stop(); Console.WriteLine("{0} {1}", "time elapsed", timer.Elapsed.TotalSeconds.ToString()); } catch (AggregateException e) { Console.WriteLine(e.Message.ToString()); } } // hard-coded data for correlation matrix static double[,] createCorrelationMatrix() { double[,] correlation = new double[5, 5]; correlation[0, 0] = 1.0; correlation[0, 1] = 0.748534249620189; correlation[0, 2] = 0.751; correlation[0, 3] = 0.819807151586399; correlation[0, 4] = 0.296516443152486; correlation[1, 0] = 0.748534249620189; correlation[1, 1] = 1.0; correlation[1, 2] = 0.630062355599386; correlation[1, 3] = 0.715491543000545; correlation[1, 4] = 0.329358787086333; correlation[2, 0] = 0.751; correlation[2, 1] = 0.630062355599386; correlation[2, 2] = 1.0; correlation[2, 3] = 0.758158276137995; correlation[2, 4] = 0.302715778081627; correlation[3, 0] = 0.819807151586399; correlation[3, 1] = 0.715491543000545; correlation[3, 2] = 0.758158276137995; correlation[3, 3] = 1.0; correlation[3, 4] = 0.286336231914179; correlation[4, 0] = 0.296516443152486; correlation[4, 1] = 0.329358787086333; correlation[4, 2] = 0.302715778081627; correlation[4, 3] = 0.286336231914179; correlation[4, 4] = 1.0; return correlation; } } // ******************************************************************** // // consumer class for correlated random numbers public class Consumer { public event MatrixReceiver ReceiveMatrix; public string ID; private int n; // public Consumer(int n, string ID) { this.n = n; this.ID = ID; } public void Process() { for (int i = 0; i < n; i++) { // get correlated 1xM random matrix from CopulaQueue and print it to console double[,] matrix = ReceiveMatrix(); Console.WriteLine("{0} {1} {2} {3} {4} {5}", this.ID, Math.Round(matrix[0, 0], 4), Math.Round(matrix[0, 1], 4), Math.Round(matrix[0, 2], 4), Math.Round(matrix[0, 3], 4), Math.Round(matrix[0, 4], 4)); // } } } // ******************************************************************** // // abstract base class for all uniform random generators public abstract class RandomGenerator { public abstract double GetUniformRandom(); } // ******************************************************************** // // uniform random generator implementation by using CSharp Random class public class CSharpRandom : RandomGenerator { private Random generator; // public CSharpRandom() { // using unique GUID hashcode as a seed generator = new Random(Guid.NewGuid().GetHashCode()); } public override double GetUniformRandom() { // Random.NextDouble method returns a double greater than or equal to 0.0 // and less than 1.0. Built-in checking procedure prevents out-of-bounds random // number to be re-distributed further to CopulaEngine implementation. double rand = 0.0; while (true) { rand = generator.NextDouble(); if (rand > 0.0) break; } return rand; } } // ******************************************************************** // // abstract base class for all specific copula implementations public abstract class CopulaEngine { // Uniform random generator and correlation matrix are hosted in this abstract base class. // Concrete classes are providing algorithm implementation for a specific copula // and event mechanism for sending created correlated random numbers matrix data to CopulaQueue class. protected RandomGenerator generator; protected double[,] correlation; // public CopulaEngine(double[,] correlation, RandomGenerator generator) { this.correlation = correlation; this.generator = generator; } public abstract void Process(); } // ******************************************************************** // // concrete implementation for gaussian copula public class GaussianCopula : CopulaEngine { public event MatrixSender SendMatrix; private double[,] normalRandomMatrix; private double[,] choleskyMatrix; private double[,] correlatedNormalRandomMatrix; private double[,] correlatedUniformRandomMatrix; private int rows; private int cols; // public GaussianCopula(int n, double[,] correlation, RandomGenerator generator) : base(correlation, generator) { this.cols = base.correlation.GetUpperBound(0) + 1; // M, number of variables this.rows = n; // N, number of 1xM matrices } public override void Process() { // NxM matrix containing of uniformly distributed correlated random variables are calculated // as a sequence of specific matrix operations createNormalRandomMatrix(); createCholeskyMatrix(); correlatedNormalRandomMatrix = MatrixTools.Transpose(MatrixTools.Multiplication(choleskyMatrix, MatrixTools.Transpose(normalRandomMatrix))); createCorrelatedUniformRandomMatrix(); } private void createNormalRandomMatrix() { // create NxM matrix consisting of normally distributed independent random variables normalRandomMatrix = new double[rows, cols]; for (int i = 0; i < rows; i++) { for (int j = 0; j < cols; j++) { normalRandomMatrix[i, j] = StatTools.NormSInv(base.generator.GetUniformRandom()); } } } private void createCholeskyMatrix() { // create lower-triangular NxM cholesky decomposition matrix choleskyMatrix = new double[cols, cols]; double s = 0.0; // for (int j = 1; j <= cols; j++) { s = 0.0; for (int k = 1; k <= (j - 1); k++) { s += Math.Pow(choleskyMatrix[j - 1, k - 1], 2.0); } choleskyMatrix[j - 1, j - 1] = base.correlation[j - 1, j - 1] - s; if (choleskyMatrix[j - 1, j - 1] <= 0.0) break; choleskyMatrix[j - 1, j - 1] = Math.Sqrt(choleskyMatrix[j - 1, j - 1]); // for (int i = j + 1; i <= cols; i++) { s = 0.0; for (int k = 1; k <= (j - 1); k++) { s += (choleskyMatrix[i - 1, k - 1] * choleskyMatrix[j - 1, k - 1]); } choleskyMatrix[i - 1, j - 1] = (base.correlation[i - 1, j - 1] - s) / choleskyMatrix[j - 1, j - 1]; } } } private void createCorrelatedUniformRandomMatrix() { // map normally distributed numbers back to uniform plane // process NxM matrix row by row for (int i = 0; i < rows; i++) { // create a new 1xM matrix for each row and perform uniform transformation correlatedUniformRandomMatrix = new double[1, cols]; for (int j = 0; j < cols; j++) { correlatedUniformRandomMatrix[0, j] = StatTools.NormSDist(correlatedNormalRandomMatrix[i, j]); } // event : send transformed 1xM matrix to CopulaQueue this.SendMatrix(correlatedUniformRandomMatrix); } } } // ******************************************************************** // // this is technically just a wrapper class for ConcurrentQueue data structure public class CopulaQueue { private ConcurrentQueue<double[,]> queue; public CopulaQueue() { queue = new ConcurrentQueue<double[,]>(); } public void Enqueue(double[,] matrix) { // insert a matrix into data structure queue.Enqueue(matrix); } public double[,] Dequeue() { // remove a matrix from data structure double[,] matrix = null; bool hasValue = false; while (!hasValue) hasValue = queue.TryDequeue(out matrix); return matrix; } } // ******************************************************************** // // collection of methods for different types of statistical calculations public static class StatTools { // rational approximation for the inverse of standard normal cumulative distribution. // the distribution has a mean of zero and a standard deviation of one. // source : Peter Acklam web page home.online.no/~pjacklam/notes/invnorm/ public static double NormSInv(double x) { const double a1 = -39.6968302866538; const double a2 = 220.946098424521; const double a3 = -275.928510446969; const double a4 = 138.357751867269; const double a5 = -30.6647980661472; const double a6 = 2.50662827745924; // const double b1 = -54.4760987982241; const double b2 = 161.585836858041; const double b3 = -155.698979859887; const double b4 = 66.8013118877197; const double b5 = -13.2806815528857; // const double c1 = -7.78489400243029E-03; const double c2 = -0.322396458041136; const double c3 = -2.40075827716184; const double c4 = -2.54973253934373; const double c5 = 4.37466414146497; const double c6 = 2.93816398269878; // const double d1 = 7.78469570904146E-03; const double d2 = 0.32246712907004; const double d3 = 2.445134137143; const double d4 = 3.75440866190742; // const double p_low = 0.02425; const double p_high = 1.0 - p_low; double q = 0.0; double r = 0.0; double c = 0.0; // if ((x > 0.0) && (x < 1.0)) { if (x < p_low) { // rational approximation for lower region q = Math.Sqrt(-2.0 * Math.Log(x)); c = (((((c1 * q + c2) * q + c3) * q + c4) * q + c5) * q + c6) / ((((d1 * q + d2) * q + d3) * q + d4) * q + 1); } if ((x >= p_low) && (x <= p_high)) { // rational approximation for middle region q = x - 0.5; r = q * q; c = (((((a1 * r + a2) * r + a3) * r + a4) * r + a5) * r + a6) * q / (((((b1 * r + b2) * r + b3) * r + b4) * r + b5) * r + 1); } if (x > p_high) { // rational approximation for upper region q = Math.Sqrt(-2 * Math.Log(1 - x)); c = -(((((c1 * q + c2) * q + c3) * q + c4) * q + c5) * q + c6) / ((((d1 * q + d2) * q + d3) * q + d4) * q + 1); } } else { // throw if given x value is out of bounds (less or equal to 0.0, greater or equal to 1.0) throw new Exception("input parameter out of bounds"); } return c; } public static double NormSDist(double x) { // returns the standard normal cumulative distribution function. // the distribution has a mean of zero and a standard deviation of one. double sign = 1.0; if (x < 0) sign = -1.0; return 0.5 * (1.0 + sign * errorFunction(Math.Abs(x) / Math.Sqrt(2.0))); } private static double errorFunction(double x) { // uses Hohner's method for improved efficiency. const double a1 = 0.254829592; const double a2 = -0.284496736; const double a3 = 1.421413741; const double a4 = -1.453152027; const double a5 = 1.061405429; const double a6 = 0.3275911; x = Math.Abs(x); double t = 1 / (1 + a6 * x); return 1 - ((((((a5 * t + a4) * t) + a3) * t + a2) * t) + a1) * t * Math.Exp(-1 * x * x); } } // ******************************************************************** // // collection of methods for different types of matrix operations public static class MatrixTools { public static double[,] Transpose(double[,] matrix) { // method for transposing matrix double[,] result = new double[matrix.GetUpperBound(1) + 1, matrix.GetUpperBound(0) + 1]; // for (int i = 0; i < matrix.GetUpperBound(0) + 1; i++) { for (int j = 0; j < matrix.GetUpperBound(1) + 1; j++) { result[j, i] = matrix[i, j]; } } return result; } public static double[,] Multiplication(double[,] matrix1, double[,] matrix2) { // method for matrix multiplication double[,] result = new double[matrix1.GetUpperBound(0) + 1, matrix2.GetUpperBound(1) + 1]; double v = 0.0; // for (int i = 0; i < matrix1.GetUpperBound(0) + 1; i++) { for (int j = 0; j < matrix2.GetUpperBound(1) + 1; j++) { v = 0.0; for (int k = 0; k < matrix1.GetUpperBound(1) + 1; k++) { v += matrix1[i, k] * matrix2[k, j]; } result[i, j] = v; } } return result; } } }
TEST RUN
When running the program, I get the following console printout. The printout shows, how our four consumers used in the example program are Dequeueing correlated 1x5 random matrices from CopulaQueue in parallel.EFFICIENCY AND CORRELATION
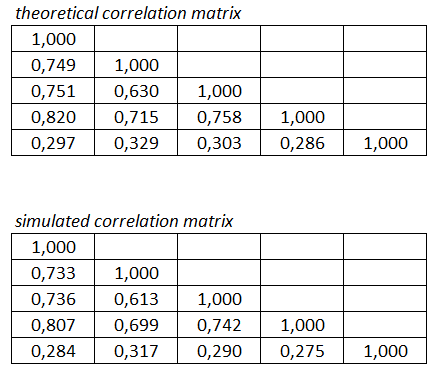
One million rows for 5x5 correlation matrix was processed 100 times, when testing efficiency of the producer part of the program. More specifically, four producers (CopulaEngine) are creating 1x5 matrices, consisting of five correlated uniformly distributed random numbers one by one and then sending these matrices to ConcurrentQueue wrapped in CopulaQueue class in parallel. Each of the four producers are then performing this operation 250 thousand times. Finally, the whole operation was repeated 1 hundred times and time elapsed for each repetition was saved for further analysis. The results of this experiment are reported in the table below.As we can see in the table, multi-threading is nicely reducing processing time, but in a non-linear fashion. Next, I printed out one batch of correlated random numbers (1000000x5 matrix) into text file and compared theoretical and simulated correlation in Excel. Results are reported in the table below. We can see, that simulated correlation is in line with theoretical correlation (enough, IMHO).
READING REFERENCES
For me personally, the following two books are standing in their own class. Ben and Joseph Albahari C# in a nutshell is presenting pretty much everything one has to know (and a lot more) about C# and especially on .NET framework. Very nice thing is also, that Albahari brothers have been kindly offering a free chapter on multi-threading from this book on their website. Daniel Duffy and Andrea Germani C# for financial markets is presenting how to apply C# in financial programs. There are a lot of extremely useful examples on multi-threaded programs, especially on using multi-threading in Monte Carlo applications and the general usage of Producer-Consumer pattern, when using multi-threading.
Again, Big thanks for reading my blog and Happy and Better New Year 2015 for everybody.
-Mike
-Mike





.png)

.png)
.png)
.png)

.png)
.png)

.png)
.png)
.png)
.png)