FINAL DESTINATION
The circle has been closed. This post is kind of an aggregation, based on the last four posts published on generating random numbers. Initially, I started just with a simple template class for distributional random generator, then continued with a path generator using any one-factor stochastic process and finally, ended up with a multi-threaded distributional random generation scheme using Parallel algorithms. This final post (hopefully) is opening up my larger goal : to be able to generate asset price paths for any one-factor process, using multi-threading scheme.
GROUNDHOG DAY
Again, I have tested the both sequential (for_each) and parallel (parallel_for_each) schemes by using four generators, 10000 paths and 250 time steps for a single run. After this, I repeated this run for 250 times. Conclusion :
- The average running time for this sample was 17116 milliseconds (sequential) and 8209 milliseconds (parallel). So, parallel scheme will be completed about two times faster.
- The actual CPU usage profiles during the simulation processes are behaving exactly as reported in this post.
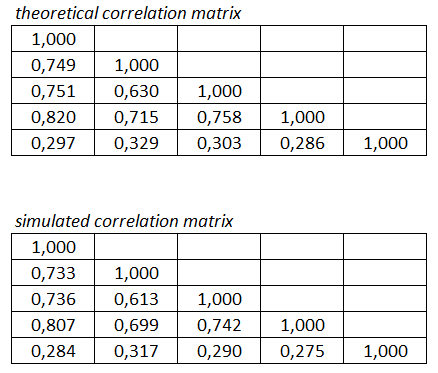
- I also analyzed processed asset price paths for parallel scheme, just to be absolutely sure there are no path duplicates (random number generation would not be independent). Based on my analysis made in Excel, all processed asset price paths are different and there are no duplicates.
Presented scheme for path generator is again fulfilling my two initial requirements : faster creation of asset price paths following any one-factor process and independency of random generators.
RandomGenerator.h
The basic functionality of this template class has not been changed, except for construction part : second constructor is allowing a client to give any probability distribution for uniform generator from outside of this class. Even there is actually no need for having this kind of optionality in real-life (most of the stuff in Monte Carlo is randomized by using standard normal distribution), I decided to implement this optionality for the sake of completeness.
#pragma once #include <algorithm> #include <functional> #include <vector> #include <random> #include <memory> // namespace MikeJuniperhillRandomGeneratorTemplate { template <typename Generator = std::mt19937, typename Distribution = std::normal_distribution<double>> /// <summary> /// Template class for creating random number paths using mt19937 as default uniform /// random generator and Standard Normal as default probability distribution. /// </summary> class RandomGenerator { public: /// <summary> /// Constructor with explicit seed value /// </summary> RandomGenerator(unsigned long seed) { // construct function for processing distributional random number randomGenerator = [this](double x)-> double { x = distribution(uniformGenerator); return x; }; // seed generator once uniformGenerator.seed(seed); } /// <summary> /// Constructor for explicit seed value and client-given probability distribution. /// </summary> RandomGenerator(unsigned long seed, const Distribution& distribution) // constructor delegation : RandomGenerator(seed) { // assign client-given probability distribution this->distribution = distribution; } /// <summary> /// Fill a given vector reference with distributional random numbers /// </summary> void operator()(std::vector<double>& v) const { std::transform(v.begin(), v.end(), v.begin(), randomGenerator); } private: std::function<double(double)> randomGenerator; Generator uniformGenerator; Distribution distribution; }; } //
OneFactorProcess.h
I decided to tag drift and diffusion functions with const declaration, since these functions should not modify the internal state of class data members.
#pragma once // namespace MikeJuniperhillOneFactorProcessLibrary { /// <summary> /// Abstract base class for all one-factor processes for customizing /// drift and diffusion functions for different types of processes. /// </summary> class OneFactorProcess { public: virtual double drift(double x, double t) const = 0; virtual double diffusion(double x, double t) const = 0; }; // /// <summary> /// Implementation for Vasicek short-rate model. /// </summary> class Vasicek : public OneFactorProcess { public: Vasicek(double meanReversion, double longTermRate, double rateVolatility) : meanReversion(meanReversion), longTermRate(longTermRate), rateVolatility(rateVolatility) { } // double drift(double x, double t) const override { return meanReversion * (longTermRate - x); } double diffusion(double x, double t) const override { return rateVolatility; } private: double meanReversion; double longTermRate; double rateVolatility; }; } //
PathGenerator.h
As in the case with RandomGenerator, the basic functionality of this template class has not been changed either, except for construction part : second constructor is allowing a client to give any probability distribution to be delivered for distributional random generator.
#pragma once // #include "RandomGenerator.h" #include "OneFactorProcess.h" namespace MJRandom = MikeJuniperhillRandomGeneratorTemplate; namespace MJProcess = MikeJuniperhillOneFactorProcessLibrary; // namespace MikeJuniperhillPathGenerator { template <typename Generator = std::mt19937, typename Distribution = std::normal_distribution<double>> class PathGenerator { public: /// <summary> /// Constructor for PathGenerator template class. /// </summary> PathGenerator(double spot, double maturity, unsigned long seed, const std::shared_ptr<MJProcess::OneFactorProcess>& process) : spot(spot), maturity(maturity), process(process) { // create random generator generator = std::unique_ptr<MJRandom::RandomGenerator<Generator, Distribution>> (new MJRandom::RandomGenerator<Generator, Distribution>(seed)); } /// <summary> /// Constructor for PathGenerator template class, with a client-given probability distribution /// </summary> PathGenerator(double spot, double maturity, unsigned long seed, const std::shared_ptr<MJProcess::OneFactorProcess>& process, const Distribution& distribution) : spot(spot), maturity(maturity), process(process) { // create random generator with client-given probability distribution generator = std::unique_ptr<MJRandom::RandomGenerator<Generator, Distribution>> (new MJRandom::RandomGenerator<Generator, Distribution>(seed, distribution)); } /// <summary> /// Fill a given vector reference with asset prices, following a given stochastic process. /// </summary> void operator()(std::vector<double>& v) const { // transform initialized vector into a path containing random numbers (*generator)(v); // double dt = maturity / (v.size() - 1); double dw = 0.0; double s = spot; double t = 0.0; v[0] = s; // 1st path element will always be the current spot price // // transform distributional random number vector into a path containing // asset prices from a given stochastic one-factor process for (auto it = v.begin() + 1; it != v.end(); ++it) { t += dt; dw = (*it) * std::sqrt(dt); (*it) = s + (*process).drift(s, t) * dt + (*process).diffusion(s, t) * dw; s = (*it); } } private: double spot; double maturity; std::shared_ptr<MJProcess::OneFactorProcess> process; std::unique_ptr<MJRandom::RandomGenerator<Generator, Distribution>> generator; }; } //
Tester.cpp
Tester program is closely tracking the program presented in previous post. For the sake of additional clarity, I have used new type definitions in order to improve code readability and get rid of some lengthy variable names. The program is again using simple factory method for creating PathGenerator (function wrapped in shared pointer). In this program, OneFactorProcess implementation is created and delivered for factory method for processing. Finally, there is a method for printing processed paths to console for testing purposes.
#include <iostream> #include <chrono> #include <ppl.h> #include <concurrent_vector.h> #include "PathGenerator.h" namespace MJGenerator = MikeJuniperhillPathGenerator; // // type definitions using Path = std::vector<double>; using Paths = concurrency::concurrent_vector<Path>; using Process = std::shared_ptr<MJProcess::OneFactorProcess>; using Processor = std::function<void(void)>; using PathGenerator = std::shared_ptr<Processor>; // // thread-safe container for storing asset price paths, processed by path generators Paths paths; // // printer for generated asset price paths void Printer() { std::for_each(paths.begin(), paths.end(), [](Path path) -> void { std::for_each(path.begin(), path.end(), [](double s) -> void { std::cout << s << ","; }); std::cout << std::endl; }); } // // factory method : // return path-generating function as function wrapper // input arguments are common for all types of generators PathGenerator Factory(double spot, double maturity, int nPaths, int nSteps, unsigned long seed, const Process& process, Paths& paths) { // create function for processing one-factor paths auto generator = [=, &process, &paths]() -> void { MJGenerator::PathGenerator<> oneFactorProcess(spot, maturity, seed, process); Path path(nSteps); for (auto i = 0; i != nPaths; ++i) { oneFactorProcess(path); paths.push_back(path); } }; // return generator function as function wrapper return PathGenerator(new Processor(generator)); } // int main() { // create vasicek process double longTermRate = 0.05; double meanReversion = 0.2; double rateVolatility = 0.0075; Process vasicek = Process(new MJProcess::Vasicek(meanReversion, longTermRate, rateVolatility)); // // define parameters and seed values for path generators int nGenerators = 4; int nPaths = 100; int nSteps = (250 + 1); std::vector<unsigned long> seed = { 10322854, 65947, 387528, 772399573 }; // // use factory method for creating path generators double spot = 0.0095; double maturity = 3.0; std::vector<PathGenerator> generators; for (auto i = 0; i < nGenerators; i++) generators.push_back( Factory(spot, maturity, nPaths, nSteps, seed[i], vasicek, paths)); // // parallel processing auto start = std::chrono::steady_clock::now(); concurrency::parallel_for_each(generators.begin(), generators.end(), [](PathGenerator pg) -> void { (*pg)(); }); auto end = std::chrono::steady_clock::now(); auto timeElapsed = std::chrono::duration_cast<std::chrono::milliseconds>(end - start); std::cout << timeElapsed.count() << std::endl; // // print paths Printer(); return 0; } //
Finally, thanks again for reading this blog.
-Mike