MoCaX: Using Chebyshev Tensors for Computational Bottlenecks in Risk Calculations

Even this Machine Learning has been the hottest hype already for years, I have personally still had very vague understanding of how this thing could be applied in risk management domain. This post is presenting one such application: Chebyshev Tensors for getting rid of computational bottlenecks in risk calculations.

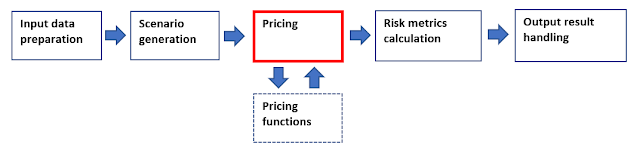
All risk management people are familiar with the following generic steps.

The sequence is describing steps for the most types of computationally-intensive risk calculations. In here, pricing (revaluation of financial transactions) is the step, which makes these calculations computationally intensive, since there will usually be substantial amount of revaluation calls sent to all kinds of pricing functions. For this reason, processing times will usually explode and this will costs us time.

In the past, the banks have usually tried to resolve these computational bottlenecks by acquiring more computational muscle and relying on multi-processing schemes. However, for a large enough player with an active derivatives book containing exotic products, even these attempts might not be enough to resolve the issue. Since the burden of producing all kinds of regulatory measures seems to be just growing, there is simply more calculations to be processed, than we have hours within one day.

Chebyshev Tensors

Another way to resolve such computational issues is to find clever algorithmic approximations and that's where Chebyshev Tensors are amazing. In a nutshell, by using Chebyshev Tensors we can create extremely accurate replicas of our standard pricing functions and use them instead of our original time-consuming function in calculations..

Interpolation methods through polynomials can deliver exponential convergence to the original function, when the interpolating points are Chebyshev points. Also, derivatives of the polynomial converge exponentially to the derivatives of the original function. Finally, Chebyshev Tensors can be extended to higher dimensions.

Example: 1-dimensional MoCaX approximation on valuing European call options

First, let us value a portfolio of European call options, where the spot price varies between 50 and 150. We divide this spot price range into one million steps. Other parameters in the model are constants. We get total of one million calculation tasks and one million revaluation calls to our pricing function. Note, that processing time is about 330 seconds (5.5 minutes) to complete all calculations. 

Next, we calculate the approximations for exactly the same set of option values, but we give only 25 analytically-valued option values for Mocax object and the rest of the values will be interpolated by Mocax object. Processing time is about 5.2 seconds to complete all calculation. Maximum error is around 1.5e-12, which is already quite close to machine precision. Error function (analytical values minus approximated values) is shown below. 

So, with just 25 Chebyshev points in our grid, we get remarkably close to the original pricing function values just with the fraction of original processing time. I dare to describe this as nothing less than impressive. This simple example just quickly scratches the surface, since one can imagine the application areas in risk management calculations are endless. Some of these application areas are well described in the book by Ignacio Ruiz and Mariano Zeron.

Let us go through the code. First, we need to import MoCaX library.

import mocaxpy

After this, we create MoCax object. In constructor, the first argument could be a callable function, but in here we just pass None, since the actual values will be delivered to our model on a later stage. The second argument is the number of dimensions. Since in our pricing function we only change the spot price and all the other variables are being fixed, our model is one-dimensional. The third argument is constructed MocaxDomain object, which sets the domain for our model. In the fourth argument, we can set our error threshold, but in here we just pass None. The fifth argument is constructed MocaxNs object, which sets the accuracy for our model.

n_dimension = 1
n_chebyshev_points = 25
domain = mocaxpy.MocaxDomain([[lowest_spot, highest_spot]])
accuracy = mocaxpy.MocaxNs([n_chebyshev_points])
mocax = mocaxpy.Mocax(None, n_dimension, domain, None, accuracy)

At it's current state, our constructed (but still incomplete) Mocax object is only aware of dimensionality, domain and grid of Chebyshev points. The next step is to set the actual function values for each point in our Chebyshev grid. 

chebyshev_points = mocax.get_evaluation_points()
option_values_at_evaluation_points = [call_option(point[0], 100.0, 1.0, 0.25, 0.01) for point in chebyshev_points]
mocax.set_original_function_values(option_values_at_evaluation_points)
call_options_approximations = [mocax.eval([spot], derivativeId=0) for spot in spots]

First, we request back the information on Chebyshev grid points (total of 25 points) from Mocax object. We need to calculate function values for all these points, since we did not give any callable pricing function in our constructor. Next, we ask revaluations from the original pricing function for all Chebyshev grid points (total of 25 revaluations). Then, we handle these calculated values back to Mocax object. Finally, we request call option values from Mocax object. As a response, we will get one million values back from Mocax object: 25 of those values were being explicitly calculated by using original pricing function and the rest are being interpolated by Mocax object.

The complete example program for this section can be found in my GitHub page.

Example: 2-dimensional MoCaX approximation on valuing European call options

Again, let us value a portfolio of European call options, but this time by changing two variables: spot price and time to maturity. Spot price varies between 50 and 150 and time to maturity varies between 0.25 and 2.5. By dividing the both domains into one thousand steps, we get grid containing one million points and for full revaluation we get total of one million calls to our pricing function. As a result, we get the familiar 3D surface.

Processing time is about 330 seconds (5.5 minutes) to complete all calculations. 

Next, we calculate the approximations for option values by using Mocax object and 25 Chebyshev points for the both domains. Revaluation calls are being sent for 625 options and the rest will be interpolated by Mocax object. Processing time is about 13.7 seconds to complete all calculation. So, with just 625 Chebyshev points in our grid, we get remarkably close to the original pricing function values just with the fraction of original processing time. Error surface is shown below (maximum error is around 7.7e-08).

 

The complete example program for this section can be found in my GitHub page.

Further material

The main source for all information is MoCaX Intelligence company page and their collection of high-quality YouTube videos. 

The book "Machine Learning for Risk Calculations: A Practitioner's View" written by Ignacio Ruiz and Mariano Zeron is also available for sale.

QuantsHub YouTube channel is also containing 1-hour video on MoCaX, as presented by Ignacio Ruiz. Concerning the material presented in this post, the most essential videos to get started on using MoCaX as presented by Mariano Zeron can be found in here and in here.

The actual MoCaX library (C++ and Python) can be downloaded from software page. The downloaded package is professionally equipped with MoCaX API documentation (doxygen), as well as with program examples and PDF documentations explaining installation and the main usage of MoCaX API. 

Thanks for reading this blog.

-Mike

QuantLib-Python: Monte Carlo Valuation for Power Reverse Dual-Currency Note (PRDC)

PRDC note

Essentially, PRDC note can be thought as taking a leveraged position on FX forward curve. Floating coupon rate is a function of FX rates, usually defined as follows.

Additional FX term (at t=0) will scale FX rate used in coupon and is usually set to be equal to FX forward at inception. Mathematically, this changes the slope of coupon payoff and therefore, adding desired leverage to the product.

Model for FX stochastics

From pricing perspective, we need to get a view on FX forward curve. This can be simulated by using Garman-KohlHagen stochastic process for an exchange rate, which is available in QuantLib-Python library. In essence, this process is Geometric Brownian Motion, with an added term for foreign interest rate. We will use this model, even it does not necessarily fully reflect the statistical properties of exchange rate.

Applying Ito's rule to Geometric Brownian Motion, gives us the following solution for an exchange rate S observed at time t.

Python program

In order to implement completely new instrument and corresponding new pricing engine in QuantLib, one should first implement these in QuantLib C++ library by following carefully the designed Instrument-Engine scheme and then, interface these newly created C++ types back to Python by using swig. However in here, we will skip the previous approach completely. Instead, we just take "all the useful bits and pieces" available in QuantLib-Python library and use these to implement our own valuation code.

QuantLib-Python object building documentation by David Duarte is available in here.

The complete code is available in here.

Libraries

The following two libraries are being used.

import numpy as np import QuantLib as ql

FX path generator

Path generator implements spot rate simulation, based on a given 1D stochastic process. Generated path is exactly in line with the dates given in coupon schedule. Note, that the exact number of paths to be generated has not been defined in this class. Whoever will be the client for this class, can request as many paths as desired. 

class PathGenerator:
    def __init__(self, valuation_date, coupon_schedule, day_counter, process):        
        self.valuation_date = valuation_date
        self.coupon_schedule = coupon_schedule
        self.day_counter = day_counter
        self.process = process
        #
        self.create_time_grids()
        
    def create_time_grids(self):
        all_coupon_dates = np.array(self.coupon_schedule)
        remaining_coupon_dates = all_coupon_dates[all_coupon_dates > self.valuation_date]
        self.time_grid = np.array([self.day_counter.yearFraction(self.valuation_date, date) 
            for date in remaining_coupon_dates])
        self.time_grid = np.concatenate((np.array([0.0]), self.time_grid))
        self.grid_steps = np.diff(self.time_grid)
        self.n_steps = self.grid_steps.shape[0]
        
    def next_path(self):
        e = np.random.normal(0.0, 1.0, self.n_steps)
        spot = self.process.x0()
        dw = e * self.grid_steps
        path = np.zeros(self.n_steps, dtype=float)
        
        for i in range(self.n_steps):
            dt = self.grid_steps[i]
            t = self.time_grid[i]
            spot = self.process.evolve(t, spot, dt, dw[i])
            path[i] = spot

        return path

Monte Carlo pricer

Monte Carlo pricer class will use path generator for simulating requested number of FX paths. A call for method npv will trigger coupon rates simulation. Simulated rates will then be corrected by taking into account of intro coupon. Finally, a series of cash flows will be created, based on calculated coupon rates and schedule dates.

class MonteCarloPricerPRDC: def __init__(self, valuation_date, coupon_schedule, day_counter, notional, discount_curve_handle, payoff_function, fx_path_generator, n_paths, intro_coupon_schedule, intro_coupon_rate): self.valuation_date = valuation_date self.coupon_schedule = coupon_schedule self.day_counter = day_counter self.notional = notional self.discount_curve_handle = discount_curve_handle self.payoff_function = payoff_function self.fx_path_generator = fx_path_generator self.n_paths = n_paths self.intro_coupon_schedule = intro_coupon_schedule self.intro_coupon_rate = intro_coupon_rate # self.create_coupon_dates() def create_coupon_dates(self): self.all_coupon_dates = np.array(self.coupon_schedule) self.past_coupon_dates = self.all_coupon_dates[self.all_coupon_dates < self.valuation_date] n_past_coupon_dates = self.past_coupon_dates.shape[0] - 1 self.past_coupon_rates = np.full(n_past_coupon_dates, 0.0, dtype=float) self.remaining_coupon_dates = self.all_coupon_dates[self.all_coupon_dates > self.valuation_date] self.time_grid = np.array([self.day_counter.yearFraction(self.valuation_date, date) for date in self.remaining_coupon_dates]) self.grid_steps = np.concatenate((np.array([self.time_grid[0]]), np.diff(self.time_grid))) self.n_steps = self.grid_steps.shape[0] if(self.intro_coupon_schedule==None): self.has_intro_coupon = False else: self.intro_coupon_dates = np.array(self.intro_coupon_schedule) self.remaining_intro_coupon_dates = self.intro_coupon_dates[self.intro_coupon_dates > self.valuation_date] self.n_remaining_intro_coupon_dates = self.remaining_intro_coupon_dates.shape[0] if(self.n_remaining_intro_coupon_dates > 0): self.has_intro_coupon = True else: self.has_intro_coupon = False def simulate_coupon_rates(self): self.simulated_coupon_rates = np.zeros(self.n_steps, dtype=float) for i in range(self.n_paths): path = self.fx_path_generator.next_path() for j in range(self.n_steps): self.simulated_coupon_rates[j] += self.payoff_function(path[j]) self.simulated_coupon_rates = self.simulated_coupon_rates / self.n_paths if(self.has_intro_coupon): self.append_intro_coupon_rates() self.coupon_rates = np.concatenate((self.past_coupon_rates, self.simulated_coupon_rates)) self.n_coupon_cash_flows = self.coupon_rates.shape[0] def append_intro_coupon_rates(self): for i in range(self.n_remaining_intro_coupon_dates): self.simulated_coupon_rates[i] = self.intro_coupon_rate def create_cash_flows(self): self.coupon_cash_flows = np.empty(self.n_coupon_cash_flows, dtype=ql.FixedRateCoupon) for i in range(self.n_coupon_cash_flows): self.coupon_cash_flows[i] = ql.FixedRateCoupon(self.all_coupon_dates[i+1], self.notional, self.coupon_rates[i], self.day_counter, self.all_coupon_dates[i], self.all_coupon_dates[i+1]) self.coupon_leg = ql.Leg(self.coupon_cash_flows) redemption = ql.Redemption(self.notional, self.all_coupon_dates[-1]) self.redemption_leg = ql.Leg(np.array([redemption])) def npv(self): self.simulate_coupon_rates() self.create_cash_flows() self.redemption_leg_npv = ql.CashFlows.npv(self.redemption_leg, self.discount_curve_handle, False) self.coupon_leg_npv = ql.CashFlows.npv(self.coupon_leg, self.discount_curve_handle, False) date = [payment.date() for payment in self.coupon_leg] amount = [payment.amount() for payment in self.coupon_leg] amount[-1] += self.notional pv = [ql.CashFlows.npv(np.array([payment]), self.discount_curve_handle, False) for payment in self.coupon_leg] pv[-1] += self.redemption_leg_npv self.cash_flow_table = np.array([date, amount, pv]) return self.coupon_leg_npv + self.redemption_leg_npv

Hard-coded factory

The creation of Garman-Kohlhagen process is isolated into hard-coded factory method. In here, we just use flat forward curves and non-calibrated short rate models for the sake of simplicity. For more realistic creation of the curves and model calibrations, check out this and this.

def process_factory():
    today = ql.Settings.instance().evaluationDate
    
    domestic_curve = ql.FlatForward(today, ql.QuoteHandle(ql.SimpleQuote(0.01)), ql.Actual360())
    domestic_curve = ql.YieldTermStructureHandle(domestic_curve)
    foreign_curve = ql.FlatForward(today, ql.QuoteHandle(ql.SimpleQuote(0.03)), ql.Actual360())
    foreign_curve = ql.YieldTermStructureHandle(foreign_curve)
    
    fx_vol = ql.QuoteHandle(ql.SimpleQuote(0.1))
    fx_vol_curve = ql.BlackVolTermStructureHandle(ql.BlackConstantVol(today, ql.NullCalendar(), fx_vol, ql.Actual360()))    
    fx_spot = ql.QuoteHandle(ql.SimpleQuote(133.2681))
    
    return ql.GarmanKohlagenProcess(fx_spot, foreign_curve, domestic_curve, fx_vol_curve)

Main program

Main program creates all required components (JPY discount curve, process, schedules, generator and pricer) and then requests npv and cash flow table as Numpy ndarray (indexing: [0] = coupon dates, [1] = cash flows, [2] = present values of cash flows).

today = ql.Date(11, 4, 2023)
ql.Settings.instance().evaluationDate = today

# create JPY discount curve
discount_curve = ql.FlatForward(today, ql.QuoteHandle(ql.SimpleQuote(0.005)), ql.Actual360())
discount_curve_handle = ql.YieldTermStructureHandle(discount_curve)

# create FX process
process = process_factory()

# create schedules for coupon- and intro coupon payments
effectiveDate = ql.Date(3, ql.September, 2015)
terminationDate = ql.Date(3, ql.September, 2041)
coupon_schedule = ql.MakeSchedule(effectiveDate, terminationDate, ql.Period(6, ql.Months), 
    backwards=True, calendar=ql.TARGET(), convention=ql.ModifiedFollowing)

intro_coupon_termination_date = ql.Date(3, ql.September, 2016)
intro_coupon_schedule = ql.MakeSchedule(effectiveDate, intro_coupon_termination_date, ql.Period(6, ql.Months), 
    backwards=True, calendar=ql.TARGET(), convention=ql.ModifiedFollowing)

# create FX path generator
fx_path_generator = PathGenerator(today, coupon_schedule, ql.Actual360(), process)

# create PRDC pricer
notional = 300000000.0
intro_coupon_rate = 0.022
n_paths = 10000
prdc_payoff_function = lambda fx_rate : min(max(0.122 * (fx_rate / 120.0) - 0.1, 0.0), 0.022)
prdc_pricer = MonteCarloPricerPRDC(ql.Settings.instance().evaluationDate, coupon_schedule, ql.Actual360(),notional, 
    discount_curve_handle, prdc_payoff_function, fx_path_generator, n_paths, intro_coupon_schedule, intro_coupon_rate)

# request results
npv_ccy = prdc_pricer.npv()
print('PV in CCY: {}'.format(npv_ccy))
jpy_eur = 145.3275
npv_eur = npv_ccy / jpy_eur
print('PV in EUR: {}'.format(npv_eur))
print()
print('Cash flow dates: {}'.format(prdc_pricer.cash_flow_table[0]))
print()
print('Cash flows: {}'.format(prdc_pricer.cash_flow_table[1]))
print()
print('Present values of cash flows: {}'.format(prdc_pricer.cash_flow_table[2]))

Thanks for reading this blog.

-Mike

Python: implementing Strategy design pattern without class hierarchy

The essence of Strategy design pattern is to enable algorithm selection to happen at run-time. Assume we would have the following two simple functions in a source file. Note, that the content of these functions is only a side-show. The main point of interest here is, how do we call these functions from somewhere else.

# functions.py
import numpy as np

def calculate_average(arr):
    return np.mean(arr)

def calculate_standard_deviation(arr):
    return np.std(arr)

In the main program, we need to select desired algorithm to process calculation for array input.

Hard-coded implementation

Below is kind of 'level-one' implementation for the main program. Needless to say, we are forced to modify the program as soon as any new function will be implemented in functions module and we would like to use that new function in the main program.

import functions

try:
    arr = [1, 2, 3, 4, 5]
    selection = 1

    if(selection == 1):
        result = functions.calculate_average(arr)
    elif(selection == 2):
        result = functions.calculate_standard_deviation(arr)
    else:
        raise Exception('Selected function is not implemented.')

    print(result)

except Exception as e:
    print(e)

Flexible implementation

Fortunately, there are ways to get out of such hard-coded scheme for selecting algorithm and this post is only presenting one such possibility. First, let us implement the following json configuration file. In this file, we are configuring the name of the function what we would like to use in our main program.

{
  "function_name": "calculate_standard_deviation"
}

In our new main program, we create configurations from the previous file and read function name from it. Then, by using hasattr function we check, if functions module is containing configured function. After this, we use getattr function to get reference to configured function. Finally, we will use the function and print calculation result.

import json
import functions

try:
    arr = [1, 2, 3, 4, 5]

    # create configurations
    path = '//temp/configurations.json'
    configurations = json.load(open(path, 'r'))
    function_name = configurations['function_name']

    if(hasattr(functions, function_name)):
        function = getattr(functions, function_name)
        result = function(arr)
    else:
        raise Exception('Calculation cannot be processed due to incorrect function configuration.')

    print(result)

except Exception as e:
    print(e)

Assume there would be a new function implementation in functions module and we would like to use that new function in our main program. In this flexible implementation, there would be no need to touch the main program here. Required change (run-time information of what function will be used) has now been isolated to configurations file.

From purely technical point of view, presented scheme is far from being 'traditional' Strategy pattern implementation starting from the fact, that there is no class hierarchy. However, code is receiving run-time instructions (from configurations file) for selecting a specific algorithm (from all functions available). At least for me, this is the essence of Strategy design pattern.

Finally, thanks for reading this blog.
-Mike

Python: Implementing Flexible Logging Mechanism

This post is presenting a way to implement flexible logging mechanism for Python program. However, just for the sake of being curious, I have also implemented another logging mechanism by using Observer Design Pattern. The both programs can be downloaded from my github page.

For flexible logging, I have the following two criteria:

1. Number of loggers (medium into which log feed will be written) can be chosen.
2. Log feed (which will be written into chosen medium) can be chosen, based on log levels.

Using Observer Pattern

import datetime as dt   
import enum

class LogLevel(enum.Enum):
    debug = 1
    info = 2
    warning = 3
    error = 4
    critical = 5
    
# subscriber in observer pattern, receives updates from publisher.
class LogHandler:
    def __init__(self, logging_function, log_level):
        self.logging_function = logging_function
        self.log_level = log_level
    
    # receive update from publisher
    def update_log(self, message, log_level):
        # log levels: debug=1, info=2, warning=3, error=4, critical=5
        # ex. class log level 1 will send log updates for all incoming messages
        if(self.log_level.value <= log_level.value):
            date_time_string = str(dt.datetime.now().strftime("%Y-%m-%d %H:%M:%S"))
            self.logging_function('{} {} {}'.format(date_time_string, log_level.name, message))
        
# publisher in observer pattern, send updates for subscribers.
class Logger:
    def __init__(self):
        self.log_handlers = set()
        
    def register_log_handler(self, log_handler):
        self.log_handlers.add(log_handler)
        
    def unregister_log_handler(self, log_handler):
        self.log_handlers.discard(log_handler)
    
    # send update for all registered subscribers
    def send_log_update(self, message, log_level):
        for log_handler in self.log_handlers:
            log_handler.update_log(message, log_level)  

# create publisher
logger = Logger()

# create console log handler (subscriber), receiving updates only when update message log level is greater than/equal to warning
console_log_handler = LogHandler(lambda message: print(message), LogLevel.warning)
logger.register_log_handler(console_log_handler)

# create file log handler (subscriber), receiving all possible updates
log_file = open('/home/mikejuniperhill/log.txt', 'w')
file_log_handler = LogHandler(lambda message: print(message, file=log_file), LogLevel.debug)
logger.register_log_handler(file_log_handler)

# process log updates
logger.send_log_update('sending calculation task to engine', LogLevel.debug)
logger.send_log_update('engine is processing calculation task', LogLevel.info)
logger.send_log_update('incorrect grid configurations, using backup grid settings', LogLevel.warning)
logger.send_log_update('analytical error retrieved for this calculation task', LogLevel.error)
logger.send_log_update('unable to process calculations task due to incorrect market data', LogLevel.critical)

log_file.close()

Log from processing feed is being printed to console and file, according to the chosen log levels.

Using Python Logging

Python is full of positive surprises and as one might expect, logging issues have already been thoroughly chewed by Python community. More information on in-built logging tools can be read from here. In the program, we create loggers and handlers (for console and file) by using method Initialize_logHandlers. This method uses Configurations object, which will be constructed from a given json file. The content of json configuration file is as follows.

{
  "LOGFORMATSTRING": "%(asctime)s %(levelname)-1s %(filename)-1s %(funcName)-1s %(message)s", 
  "CLEANLOGFILEBEFOREWRITE": 1, 
  "LOGFILEPATH": "/home/mikejuniperhill/log.txt",
  "CONSOLELOGLEVEL": 30,
  "FILELOGLEVEL": 10, 
  "LOGDATEFORMAT": "%d.%m.%Y %H:%M:%S",
  "LOGFILEMODE": "w"
}

The program below will create configurations object from json file, initializes logging handlers (console and file) and process small feed for logger.

import os, logging, json

class Configurations:
    inner = {}
    # read JSON configuration file to dictionary
    def __init__(self, filePathName):
        self.inner = json.load(open(filePathName))
    # return value for a given configuration key
    # 'overload' indexing operator
    def __getitem__(self, key):
        return self.inner[key.upper()]

def Initialize_logHandlers(configurations):
    # conditionally, delete the existing log file before starting to write log for this session
    if(bool(int(configurations['CleanLogFileBeforeWrite'])) == True):
        path = configurations['LogFilePath']
        if(os.path.exists(path) == True): os.remove(path)
 
    # create logger
    logger = logging.getLogger()
    logger.setLevel(logging.NOTSET)
 
    # console log handler
    c_handler = logging.StreamHandler()
    c_handler.setLevel(int(configurations['ConsoleLogLevel']))
    c_formatter = logging.Formatter(configurations['LogFormatString'], datefmt=configurations['LogDateFormat'])
    c_handler.setFormatter(c_formatter)
    logger.addHandler(c_handler)
 
    # file log handler
    f_handler = logging.FileHandler(configurations['LogFilePath'], mode=configurations['LogFileMode'], encoding=None, delay=True)
    f_handler.setLevel(int(configurations['FileLogLevel']))
    f_formatter = logging.Formatter(configurations['LogFormatString'], datefmt=configurations['LogDateFormat'])
    f_handler.setFormatter(f_formatter)
    logger.addHandler(f_handler)

# read configurations for this program
path = '/home/mikejuniperhill/configurations.json'
# create configurations object
configurations = Configurations(path)

# initialize log handlers
Initialize_logHandlers(configurations)
 
# process log updates
logging.debug('sending calculation task to engine')
logging.info('engine is processing calculation task')
logging.warning('incorrect grid configurations, using backup grid settings')
logging.error('analytical error retrieved for this calculation task')
logging.critical('unable to process calculations task due to incorrect market data')

Log from processing feed is being printed to console and file, according to the chosen log levels.

Finally, thanks for reading this blog.
-Mike

Python: Implementing Factory Method Design Pattern

Ideally, program should be closed for modifications, but open for extensions and hard-coded stuff should be avoided like plague. This is the point, where Design Patterns are usually stepping into picture. When the code base will grow enough in size and we are in charge of production-level programs, it is relatively easy to justify the usage of patterns. In this post, Python mutation of Factory Method Pattern is introduced for creating Task class objects, based on argument feed received from different types of sources. Complete program can be downloaded from my github page.

Imaginary scheme

Third-party analytical software is used for processing different types of complex calculations. One calculation request requires a set of specific arguments from the client program. Moreover, different types of requests will require different set of arguments (number of arguments, types of arguments). Before sending calculation request for analytical software, client program must collect arguments for all tasks to be processed from somewhere and we would like to leave the source for such task arguments open (json, text, console, xml, etc.).

Json source file

{
  "taskName": "ANZ.XVA",
  "taskType": "XVA",
  "paths": 1000,
  "storeExposures": "True" 
}

Text source file

taskName,RBC.PV
taskType,PV

Program

import sys, json, csv

# class for hosting calculation task-related information
# NOTE: the actual method for creating 'calculation request' is currently not implemented
class Task(object):
    def __init__(self, arguments):
        self.arguments = arguments
        
    # non-relevant dummy method, which just writes out given arguments
    def print(self):
        for k, v in self.arguments.items():
            print(k, 'is', v)
        
    @classmethod
    # factory: create task object from json file
    def from_json(cls, path)->'Task':
        arguments = json.load(open(path, 'r'))
        return cls(arguments)
    
    @classmethod
    # factory: create task object from text file
    def from_text(cls, path)->'Task':
        arguments = dict((k, v) for k, v in csv.reader(open(path, 'r')))
        return cls(arguments)
    
    @classmethod
    # factory: create task object from console input
    def from_console(cls)->'Task':
        arguments = json.loads(input())
        return cls(arguments)        

path = '/home/mikejuniperhill/json.feed/task.json'
task = Task.from_json(path)
task.print()

path = '/home/mikejuniperhill/json.feed/task.txt'
task = Task.from_text(path)
task.print()

task = Task.from_console()
# console feed string: {"taskName":"ANZ.WHATIF.XVA","taskType":"WHATIF","referenceTask":"ANZ.XVA"}
task.print()

Program output

Thanks for reading this blog.
-Mike

Python: Simulating Exposures Using Multiprocessing Pool

This post is presenting a scheme for simulating exposures for European call option on a non-dividend-paying stock by using Multiprocessing.Pool class (note: in Linux). There are several different options available when stepping into multiprocessing world, but for this specific purpose, Multiprocessing.Pool is robust enough. In a nutshell, we need to simulate a path for the underlying equity price and then calculate call option present value for each point in time. Complete program can be downloaded from my github.

Library imports

import multiprocessing as mp
import numpy as np
import scipy.stats as sc
import matplotlib.pyplot as pl
import time, math

Methods

# black scholes valuation of call option on non-dividend-paying equity
def VanillaCall(s, x, t, r, v):
    pv = 0.0
    # option value at maturity
    if((t - 0.0) < (1 / 365)):
        pv = max(s - x, 0.0)
    # option value before its maturity
    else:
        d1 = (math.log(s / x) + (r + 0.5 * v ** 2) * t) / (v * math.sqrt(t))
        d2 = (math.log(s / x) + (r - 0.5 * v ** 2) * t) / (v * math.sqrt(t))
        pv = (s * sc.norm.cdf(d1, 0.0, 1.0) - x * math.exp(-r * t) * sc.norm.cdf(d2, 0.0, 1.0))
    return pv

# globalize local parameters
def Globalizer(local_parameters):
    global global_parameters
    global_parameters = local_parameters

# simulate exposures by using
# - a given one-factor process (func_process)
# - a given pricing function (func_pricing)
def SimulateExposures(arg):
    # seed random number generator
    np.random.seed(arg)
    # unzip globalized tuple
    n_paths_per_process, n_steps, t, s_0, r, vol, func_pricing, func_process = global_parameters
    s = 0.0
    pv = 0.0
    dt = (t / n_steps)
    # create container for results
    paths = np.zeros(shape=(n_paths_per_process, n_steps + 1), dtype=float)
    for i in range(n_paths_per_process):
        s = s_0
        t_expiry = t
        # value product at path inception
        paths[i, 0] = func_pricing(s, t_expiry)
        # create array of normal random variates
        e = np.random.standard_normal(n_steps)
        for j in range(n_steps):
            s = func_process(s, e[j])
            t_expiry = (t - dt * (j + 1))
            # value product at after inception
            paths[i, j + 1] = func_pricing(s, t_expiry)
    return paths

Main program

The main program will create a pool containing two processes, which will use SimulateExposures method for calculating exposures for a call option. Method takes only random seed as its direct input argument. All the other required arguments (product- or process-related parameters) will be packed into tuple data structure, which will be globalized for each process separately in initializer method. After processing, the both worker methods will return an array of simulated exposures, which then will be aggregated into array (exposures).

t_0 = time.time()

# monte carlo parameters
n_paths = 10000
n_steps = 250
n_processes = 2
n_paths_per_process = int(n_paths / n_processes)
seeds = np.random.randint(low=1, high=999999, size=n_processes)

# product- and process-related parameters
t = 1.0
s_0 = 100.0
r = 0.05
vol = 0.15
x = 100.0
drift = ((r - 0.5 * vol * vol) * (t / n_steps))
diffusion = (vol * math.sqrt(t / n_steps))

# method for calculating pv as a function of spot and time to maturity
func_pricing = lambda s_, t_: VanillaCall(s_, x, t_, r, vol)
# method for simulating stochastic process
func_process = lambda s_, e_: s_ * math.exp(drift + diffusion * e_)

# container for storing results from worker methods
results = []

# local parameters, which will be globalized for pool workers
simulation_parameters = (n_paths_per_process, n_steps, t, s_0, r, vol, func_pricing, func_process)
pool = mp.Pool(processes=n_processes, initializer=Globalizer, initargs=(simulation_parameters,))
for r in pool.imap_unordered(SimulateExposures, seeds): results.append(r)

t_1 = time.time()
print('processing time', t_1 - t_0)

# stack results from workers into one array
exposures = np.empty(shape = (0, results[0].shape[1]))
for i in range(n_processes):
    exposures = np.vstack([exposures, results[i]])

# average of all exposures
expected_exposure = np.mean(exposures, axis=0)
pl.plot(expected_exposure)
pl.show()

Thanks for reading this blog.
-Mike

QuantLib-Python: Heston Monte Carlo Valuation for Autocallable Memory Coupon Note

In the spirit of the previous post, I was woodshedding an implementation for valuing Autocallable Memory Coupon note by using libraries available in QuantLib-Python. These products are embedding a series of out-of-the-money barrier options and for this specific reason, it is important to capture implied volatility smile by using appropriate model. For this implementation example, Heston stochastic volatility model has been used. In addition to the actual Monte Carlo algorithm and path generator, I also implemented a simple method for calibrating Heston model to volatility surface by using SciPy optimization package. The complete program can be downloaded from my GitHub page.

Autocallable Notes

Autocallable notes are path-dependent structured products, which may be linked to any index. However, this product is usually linked to equity index or equity basket. If condition called autocall barrier will be reached on any coupon date, the product will be terminated immediately, after paying back coupon (usually fixed) and notional amount. However, if the underlying index will not reach autocall barrier on a coupon date, but reaches condition called coupon barrier, only fixed coupon will be paid on notional and the product will be kept alive until maturity (or until the next autocall event). Autocallables may also have a memory, which means that if the underlying index was below coupon barrier in the previous coupon date (and there was no coupon payment), but will be above coupon barrier in the next coupon date, the product will pay all cumulated (and unpaid) coupons on notional in the next coupon date. Autocallable products are (usually) not capital protected, which means that the investor is not guaranteed to receive the initial investment. If the index fixing on a final coupon date will be below condition called protection barrier, the final redemption amount will be calculated according to specific formula and investor will lose some of the invested capital. There is an example brochure and term sheet available for this product in my GitHub page.

Library Imports

import QuantLib as ql
import numpy as np
import scipy.optimize as opt

Heston Path Generator

Below is a simple (hard-coded) method for generating paths by using Heston process for a given set of QuantLib dates, which can be unevenly distributed. A couple of notes about Heston path generation process in general. QuantLib MultiPathGenerator has to be used for simulating paths for this specific process, because "under the hood", QuantLib simulates two correlated random variates: one for the asset and another for the volatility. As a result for "one simulation round", MultiPath object will be received from generator. This MultiPath object contains generated paths for the both asset and volatility (multiPath[0] = asset path, multiPath[1] = volatility path). So, for any further purposes (say, to use simulated asset path for something), one can just use generated asset path and ignore volatility path. However, volatility path is available, if there will be some specific purpose for obtaining the information on how volatility has been evolving over time.

# hard-coded generator for Heston process
def HestonPathGenerator(dates, dayCounter, process, nPaths):
    t = np.array([dayCounter.yearFraction(dates[0], d) for d in dates])
    nGridSteps = (t.shape[0] - 1) * 2
    sequenceGenerator = ql.UniformRandomSequenceGenerator(nGridSteps, ql.UniformRandomGenerator())
    gaussianSequenceGenerator = ql.GaussianRandomSequenceGenerator(sequenceGenerator)
    pathGenerator = ql.GaussianMultiPathGenerator(process, t, gaussianSequenceGenerator, False)
    paths = np.zeros(shape = (nPaths, t.shape[0]))
    
    for i in range(nPaths):
        multiPath = pathGenerator.next().value()
        paths[i,:] = np.array(list(multiPath[0]))
        
    # return array dimensions: [number of paths, number of items in t array]
    return paths

Heston Model Calibration

Below is a simple (hard-coded) method for calibrating Heston model into a given volatility surface. Inside this method, process, model and engine are being created. After this, calibration helpers for Heston model are being created by using given volatility surface data. Finally, calibrated model and process are being returned for any further use. The actual optimization workhorse will be given outside of this method. For this specific example program, SciPy's Differential Evolution solver is being used, in order to guarantee global minimization result.

# hard-coded calibrator for Heston model
def HestonModelCalibrator(valuationDate, calendar, spot, curveHandle, dividendHandle, 
    v0, kappa, theta, sigma, rho, expiration_dates, strikes, data, optimizer, bounds):
    
    # container for heston calibration helpers
    helpers = []
    
    # create Heston process, model and pricing engine
    # use given initial parameters for model
    process = ql.HestonProcess(curveHandle, dividendHandle, 
        ql.QuoteHandle(ql.SimpleQuote(spot)), v0, kappa, theta, sigma, rho)
    model = ql.HestonModel(process)
    engine = ql.AnalyticHestonEngine(model)
    
    # nested cost function for model optimization
    def CostFunction(x):
        parameters = ql.Array(list(x))        
        model.setParams(parameters)
        error = [helper.calibrationError() for helper in helpers]
        return np.sqrt(np.sum(np.abs(error)))

    # create Heston calibration helpers, set pricing engines
    for i in range(len(expiration_dates)):
        for j in range(len(strikes)):
            expiration = expiration_dates[i]
            days = expiration - valuationDate
            period = ql.Period(days, ql.Days)
            vol = data[i][j]
            strike = strikes[j]
            helper = ql.HestonModelHelper(period, calendar, spot, strike,
                ql.QuoteHandle(ql.SimpleQuote(vol)), curveHandle, dividendHandle)
            helper.setPricingEngine(engine)
            helpers.append(helper)
    
    # run optimization, return calibrated model and process
    optimizer(CostFunction, bounds)
    return process, model

Monte Carlo Valuation

The actual Autocallable valuation algorithm has been implemented in this part of the code. For the sake of being able to value this product also after its inception, valuation method takes past fixings as Python dictionary (key: date, value: fixing). Now, if one changes valuation date to any possible date after inception and before transaction maturity, the product will also be valued accordingly. It should be noted, that in such scheme it is crucial to provide all possible past fixings. Failure to do this, will lead to an exception. Algorithm implementation is a bit long and might look scary, but it is actually really straightforward if one is familiar enough with this specific product.

def AutoCallableNote(valuationDate, couponDates, strike, pastFixings, 
    autoCallBarrier, couponBarrier, protectionBarrier, hasMemory, finalRedemptionFormula, 
    coupon, notional, dayCounter, process, generator, nPaths, curve):    
    
    # immediate exit trigger for matured transaction
    if(valuationDate >= couponDates[-1]): return 0.0
    
    # immediate exit trigger for any past autocall event
    if(valuationDate >= couponDates[0]):
        if(max(pastFixings.values()) >= (autoCallBarrier * strike)): return 0.0

    # create date array for path generator
    # combine valuation date and all the remaining coupon dates
    dates = np.hstack((np.array([valuationDate]), couponDates[couponDates > valuationDate]))
    
    # generate paths for a given set of dates, exclude the current spot rate
    paths = generator(dates, dayCounter, process, nPaths)[:,1:]
    
    # identify the past coupon dates
    pastDates = couponDates[couponDates <= valuationDate]

    # conditionally, merge given past fixings from a given dictionary and generated paths
    if(pastDates.shape[0] > 0):
        pastFixingsArray = np.array([pastFixings[pastDate] for pastDate in pastDates])        
        pastFixingsArray = np.tile(pastFixingsArray, (paths.shape[0], 1))
        paths = np.hstack((pastFixingsArray, paths))
    
    # result accumulator
    global_pv = []
    expirationDate = couponDates[-1]
    hasMemory = int(hasMemory)
    
    # loop through all simulated paths
    for path in paths:
        payoffPV = 0.0
        unpaidCoupons = 0
        hasAutoCalled = False
        
        # loop through set of coupon dates and index ratios
        for date, index in zip(couponDates, (path / strike)):
            # if autocall event has been triggered, immediate exit from this path
            if(hasAutoCalled): break
            payoff = 0.0
                
            # payoff calculation at expiration
            if(date == expirationDate):
                # index is greater or equal to coupon barrier
                # pay 100% redemption, plus coupon, plus conditionally all unpaid coupons
                if(index >= couponBarrier):
                    payoff = notional * (1 + (coupon * (1 + unpaidCoupons * hasMemory)))
                # index is greater or equal to protection barrier and less than coupon barrier
                # pay 100% redemption, no coupon
                if((index >= protectionBarrier) & (index < couponBarrier)):
                    payoff = notional
                # index is less than protection barrier
                # pay redemption according to formula, no coupon
                if(index < protectionBarrier):
                    # note: calculate index value from index ratio
                    index = index * strike
                    payoff = notional * finalRedemptionFormula(index)
                
            # payoff calculation before expiration
            else:
                # index is greater or equal to autocall barrier
                # autocall will happen before expiration
                # pay 100% redemption, plus coupon, plus conditionally all unpaid coupons
                if(index >= autoCallBarrier):
                    payoff = notional * (1 + (coupon * (1 + unpaidCoupons * hasMemory)))
                    hasAutoCalled = True
                # index is greater or equal to coupon barrier and less than autocall barrier
                # autocall will not happen
                # pay coupon, plus conditionally all unpaid coupons
                if((index >= couponBarrier) & (index < autoCallBarrier)):
                    payoff = notional * (coupon * (1 + unpaidCoupons * hasMemory))
                    unpaidCoupons = 0
                # index is less than coupon barrier
                # autocall will not happen
                # no coupon payment, only accumulate unpaid coupons
                if(index < couponBarrier):
                    payoff = 0.0
                    unpaidCoupons += 1                    

            # conditionally, calculate PV for period payoff, add PV to local accumulator
            if(date > valuationDate):
                df = curveHandle.discount(date)
                payoffPV += payoff * df
            
        # add path PV to global accumulator
        global_pv.append(payoffPV)
        
    # return PV
    return np.mean(np.array(global_pv))

Main Program

Finally, in this part of the program we will actually use the stuff presented above. First, the usual QuantLib-related parameters are being created, as well as parameters for Autocallable product. Note, that since in this example we are valuing this product at inception, there is no need to provide any past fixings for valuation method (however, it is not forbidden either). After this, interest rate curve and dividend curve will be created, as well as volatility surface data for calibration purposes. Next, initial guesses for Heston parameters will be set and the model will then be calibrated by using dedicated method. Finally, calibrated process will be given to the actual valuation method and Monte Carlo valuation will be processed.

# general QuantLib-related parameters
valuationDate = ql.Date(20,11,2019)
ql.Settings.instance().evaluationDate = valuationDate
convention = ql.ModifiedFollowing
dayCounter = ql.Actual360()
calendar = ql.TARGET()

# Autocallable Memory Coupon Note
notional = 1000000.0
spot = 3550.0
strike = 3550.0
autoCallBarrier = 1.0
couponBarrier = 0.8
protectionBarrier = 0.6
finalRedemptionFormula = lambda indexAtMaturity: min(1.0, indexAtMaturity / strike)
coupon = 0.05
hasMemory = True

# coupon schedule for note
startDate = ql.Date(20,11,2019)
firstCouponDate = calendar.advance(startDate, ql.Period(1, ql.Years))
lastCouponDate = calendar.advance(startDate, ql.Period(7, ql.Years))
couponDates = np.array(list(ql.Schedule(firstCouponDate, lastCouponDate, ql.Period(ql.Annual), 
    calendar, ql.ModifiedFollowing, ql.ModifiedFollowing, ql.DateGeneration.Forward, False)))

# create past fixings into dictionary
pastFixings = {}
#pastFixings = { ql.Date(20,11,2020): 99.0, ql.Date(22,11,2021): 99.0 }

# create discounting curve and dividend curve, required for Heston model
curveHandle = ql.YieldTermStructureHandle(ql.FlatForward(valuationDate, 0.01, dayCounter))
dividendHandle = ql.YieldTermStructureHandle(ql.FlatForward(valuationDate, 0.0, dayCounter))

# Eurostoxx 50 volatility surface data
expiration_dates = [ql.Date(19,6,2020), ql.Date(18,12,2020), 
    ql.Date(18,6,2021), ql.Date(17,12,2021), ql.Date(17,6,2022),
    ql.Date(16,12,2022), ql.Date(15,12,2023), ql.Date(20,12,2024), 
    ql.Date(19,12,2025), ql.Date(18,12,2026)]

strikes = [3075, 3200, 3350, 3550, 3775, 3950, 4050]

data = [[0.1753, 0.1631, 0.1493, 0.132 , 0.116 , 0.108 , 0.1052],
       [0.1683, 0.1583, 0.147 , 0.1334, 0.1212, 0.1145, 0.1117],
       [0.1673, 0.1597, 0.1517, 0.1428, 0.1346, 0.129 , 0.1262],
       [0.1659, 0.1601, 0.1541, 0.1474, 0.1417, 0.1381, 0.1363],
       [0.1678, 0.1634, 0.1588, 0.1537, 0.1493, 0.1467, 0.1455],
       [0.1678, 0.1644, 0.1609, 0.1572, 0.1541, 0.1522, 0.1513],
       [0.1694, 0.1666, 0.1638, 0.1608, 0.1584, 0.1569, 0.1562],
       [0.1701, 0.168 , 0.166 , 0.164 , 0.1623, 0.1614, 0.161 ],
       [0.1715, 0.1698, 0.1682, 0.1667, 0.1654, 0.1648, 0.1645],
       [0.1724, 0.171 , 0.1697, 0.1684, 0.1675, 0.1671, 0.1669]]

# initial parameters for Heston model
theta = 0.01
kappa = 0.01
sigma = 0.01
rho = 0.01
v0 = 0.01

# bounds for model parameters (1=theta, 2=kappa, 3=sigma, 4=rho, 5=v0)
bounds = [(0.01, 1.0), (0.01, 10.0), (0.01, 1.0), (-1.0, 1.0), (0.01, 1.0)]

# calibrate Heston model, print calibrated parameters
calibrationResult = HestonModelCalibrator(valuationDate, calendar, spot, curveHandle, dividendHandle, 
        v0, kappa, theta, sigma, rho, expiration_dates, strikes, data, opt.differential_evolution, bounds)
print('calibrated Heston parameters', calibrationResult[1].params())

# monte carlo parameters
nPaths = 10000

# request and print PV
PV = AutoCallableNote(valuationDate, couponDates, strike, pastFixings, 
    autoCallBarrier, couponBarrier, protectionBarrier, hasMemory, finalRedemptionFormula, 
    coupon, notional, dayCounter, calibrationResult[0], HestonPathGenerator, nPaths, curveHandle)

print(PV)

Finally, thanks for reading this blog and have a pleasant wait for the coming Christmas.
-Mike