Multi-Threaded Copula producer in C#

I wanted to publish one more article for the sake of celebrating the end of the year 2014. This time I am opening one possible solution for producing multi-threaded correlated random numbers with Gaussian Copula in C#. The numerical scheme used for this procedure has already been opened well enough in this blog posting. Usually, programs presented in this blog have been having (more or less) something to do with Microsoft Excel. This time, there is only C# program. However, with all the example programs presented in this blog, the user should be able to interface this program back to Excel in many different ways, if so desired.

PRODUCER-CONSUMER

In this simple example program, Producer-Consumer Pattern has been used. CopulaQueue class is nothing more, than just a wrapper for thread-safe ConcurrentQueue data structure. More specifically, the part of the program which actually creates all correlated random numbers into CopulaQueue, is the Producer. In the program, concrete CopulaEngine implementation class takes concrete RandomGenerator implementation class and correlation matrix as its input parameters. Concrete CopulaEngine implementation class then creates correlated random numbers and uses C# Event for sending created random number matrices to CopulaQueue. Another part of the program is the Consumer. Here, I have created a simple consumer class which simply prints created random numbers to console. Consumer class also uses C# Event for Dequeueing random number matrices from CopulaQueue. Needless to say, this (Consumer) is the part of our program, where we should be utilizing all correlated random numbers created by the Producer.

On design side, this program is closely following the program presented in the blog posting referred above. Again, the beef in this design is on its flexibility to allow any new implementations for Random generator and Copula model. Moreover, our example program is using C# Framework Parallel class method Parallel.ForEach, found under System.Threading.Tasks namespace. Example program creates four producers and consumers (both into List data structure) and using multi-threading (Parallel.ForEach) when processing correlated random numbers into/from CopulaQueue.

C# PROGRAM

In order to make everything as smooth as possible for the program replication, I have been writing all required classes in the same file. Just create a new console application and copy-paste the following program into a new .cs file.

using System;
using System.Diagnostics;
using System.Linq;
using System.Collections.Generic;
using System.Threading.Tasks;
using System.Collections.Concurrent;
//
namespace MultithreadingCopula
{
    // public delegate methods needed for sending and receiving matrix data
    public delegate void MatrixSender(double[,] matrix);
    public delegate double[,] MatrixReceiver();
    // ********************************************************************
    //
    // the main program 
    class Program
    {
        static void Main(string[] args)
        {
            try
            {
                // start timer
                Stopwatch timer = new Stopwatch();
                timer.Start();
                //
                // PRODUCER PART
                // create copula implementation, correlation matrix data and list of copula engines
                CopulaQueue copulaQueue = new CopulaQueue();
                double[,] correlationMatrix = createCorrelationMatrix();
                List<CopulaEngine> engines = new List<CopulaEngine>();
                int nEngines = 4;
                int nRandomArrays = 25000;
                for (int i = 0; i < nEngines; i++)
                {
                    engines.Add(new GaussianCopula(nRandomArrays, correlationMatrix, new CSharpRandom()));
                    ((GaussianCopula)engines[i]).SendMatrix += copulaQueue.Enqueue;
                }
                // process all copula engines (producers) in parallel
                Parallel.ForEach(engines, engine => engine.Process());
                //
                // CONSUMER PART
                // create list of consumers
                List<Consumer> consumers = new List<Consumer>();
                int nConsumers = nEngines;
                for (int i = 0; i < nConsumers; i++)
                {
                    consumers.Add(new Consumer(nRandomArrays, "consumer_" + (i + 1).ToString()));
                    consumers[i].ReceiveMatrix += copulaQueue.Dequeue;
                }
                // process all consumers in parallel
                Parallel.ForEach(consumers, consumer => consumer.Process());
                //
                // stop timer, print elapsed time to console
                timer.Stop();
                Console.WriteLine("{0}  {1}", "time elapsed", timer.Elapsed.TotalSeconds.ToString());
            }
            catch (AggregateException e)
            {
                Console.WriteLine(e.Message.ToString());
            }
        }
        // hard-coded data for correlation matrix
        static double[,] createCorrelationMatrix()
        {
            double[,] correlation = new double[5, 5];
            correlation[0, 0] = 1.0; correlation[0, 1] = 0.748534249620189;
            correlation[0, 2] = 0.751; correlation[0, 3] = 0.819807151586399;
            correlation[0, 4] = 0.296516443152486; correlation[1, 0] = 0.748534249620189;
            correlation[1, 1] = 1.0; correlation[1, 2] = 0.630062355599386;
            correlation[1, 3] = 0.715491543000545; correlation[1, 4] = 0.329358787086333;
            correlation[2, 0] = 0.751; correlation[2, 1] = 0.630062355599386;
            correlation[2, 2] = 1.0; correlation[2, 3] = 0.758158276137995;
            correlation[2, 4] = 0.302715778081627; correlation[3, 0] = 0.819807151586399;
            correlation[3, 1] = 0.715491543000545; correlation[3, 2] = 0.758158276137995;
            correlation[3, 3] = 1.0; correlation[3, 4] = 0.286336231914179;
            correlation[4, 0] = 0.296516443152486; correlation[4, 1] = 0.329358787086333;
            correlation[4, 2] = 0.302715778081627; correlation[4, 3] = 0.286336231914179;
            correlation[4, 4] = 1.0;
            return correlation;
        }
    }
    // ********************************************************************
    //
    // consumer class for correlated random numbers
    public class Consumer
    {
        public event MatrixReceiver ReceiveMatrix;
        public string ID;
        private int n;
        //
        public Consumer(int n, string ID) { this.n = n; this.ID = ID; }
        public void Process()
        {
            for (int i = 0; i < n; i++)
            {
                // get correlated 1xM random matrix from CopulaQueue and print it to console
                double[,] matrix = ReceiveMatrix();
                Console.WriteLine("{0}  {1}  {2}  {3}  {4}  {5}", this.ID, Math.Round(matrix[0, 0], 4), 
                    Math.Round(matrix[0, 1], 4), Math.Round(matrix[0, 2], 4), 
                    Math.Round(matrix[0, 3], 4), Math.Round(matrix[0, 4], 4));
                //
            }
        }
    }
    // ********************************************************************
    //
    // abstract base class for all uniform random generators
    public abstract class RandomGenerator
    {
        public abstract double GetUniformRandom();
    }
    // ********************************************************************
    //
    // uniform random generator implementation by using CSharp Random class
    public class CSharpRandom : RandomGenerator
    {
        private Random generator;
        //
        public CSharpRandom()
        {
            // using unique GUID hashcode as a seed
            generator = new Random(Guid.NewGuid().GetHashCode());
        }
        public override double GetUniformRandom()
        {
            // Random.NextDouble method returns a double greater than or equal to 0.0 
            // and less than 1.0. Built-in checking procedure prevents out-of-bounds random 
            // number to be re-distributed further to CopulaEngine implementation.
            double rand = 0.0;
            while (true)
            {
                rand = generator.NextDouble();
                if (rand > 0.0) break;
            }
            return rand;
        }
    }
    // ********************************************************************
    //
    // abstract base class for all specific copula implementations
    public abstract class CopulaEngine
    {
        // Uniform random generator and correlation matrix are hosted in this abstract base class.
        // Concrete classes are providing algorithm implementation for a specific copula
        // and event mechanism for sending created correlated random numbers matrix data to CopulaQueue class.
        protected RandomGenerator generator;
        protected double[,] correlation;
        //
        public CopulaEngine(double[,] correlation, RandomGenerator generator)
        {
            this.correlation = correlation;
            this.generator = generator;
        }
        public abstract void Process();
    }
    // ********************************************************************
    //
    // concrete implementation for gaussian copula
    public class GaussianCopula : CopulaEngine
    {
        public event MatrixSender SendMatrix;
        private double[,] normalRandomMatrix;
        private double[,] choleskyMatrix;
        private double[,] correlatedNormalRandomMatrix;
        private double[,] correlatedUniformRandomMatrix;
        private int rows;
        private int cols;
        //
        public GaussianCopula(int n, double[,] correlation, RandomGenerator generator)
            : base(correlation, generator)
        {
            this.cols = base.correlation.GetUpperBound(0) + 1; // M, number of variables
            this.rows = n; // N, number of 1xM matrices
        }
        public override void Process()
        {
            // NxM matrix containing of uniformly distributed correlated random variables are calculated 
            // as a sequence of specific matrix operations
            createNormalRandomMatrix();
            createCholeskyMatrix();
            correlatedNormalRandomMatrix = MatrixTools.Transpose(MatrixTools.Multiplication(choleskyMatrix, MatrixTools.Transpose(normalRandomMatrix)));
            createCorrelatedUniformRandomMatrix();
        }
        private void createNormalRandomMatrix()
        {
            // create NxM matrix consisting of normally distributed independent random variables
            normalRandomMatrix = new double[rows, cols];
            for (int i = 0; i < rows; i++)
            {
                for (int j = 0; j < cols; j++)
                {
                    normalRandomMatrix[i, j] = StatTools.NormSInv(base.generator.GetUniformRandom());
                }
            }
        }
        private void createCholeskyMatrix()
        {
            // create lower-triangular NxM cholesky decomposition matrix
            choleskyMatrix = new double[cols, cols];
            double s = 0.0;
            //
            for (int j = 1; j <= cols; j++)
            {
                s = 0.0;
                for (int k = 1; k <= (j - 1); k++)
                {
                    s += Math.Pow(choleskyMatrix[j - 1, k - 1], 2.0);
                }
                choleskyMatrix[j - 1, j - 1] = base.correlation[j - 1, j - 1] - s;
                if (choleskyMatrix[j - 1, j - 1] <= 0.0) break;
                choleskyMatrix[j - 1, j - 1] = Math.Sqrt(choleskyMatrix[j - 1, j - 1]);
                //
                for (int i = j + 1; i <= cols; i++)
                {
                    s = 0.0;
                    for (int k = 1; k <= (j - 1); k++)
                    {
                        s += (choleskyMatrix[i - 1, k - 1] * choleskyMatrix[j - 1, k - 1]);
                    }
                    choleskyMatrix[i - 1, j - 1] = (base.correlation[i - 1, j - 1] - s) / choleskyMatrix[j - 1, j - 1];
                }
            }
        }
        private void createCorrelatedUniformRandomMatrix()
        {
            // map normally distributed numbers back to uniform plane
            // process NxM matrix row by row
            for (int i = 0; i < rows; i++)
            {
                // create a new 1xM matrix for each row and perform uniform transformation
                correlatedUniformRandomMatrix = new double[1, cols];
                for (int j = 0; j < cols; j++)
                {
                    correlatedUniformRandomMatrix[0, j] = StatTools.NormSDist(correlatedNormalRandomMatrix[i, j]);
                }
                // event : send transformed 1xM matrix to CopulaQueue
                this.SendMatrix(correlatedUniformRandomMatrix);
            }
        }
    }
    // ********************************************************************
    //
    // this is technically just a wrapper class for ConcurrentQueue data structure
    public class CopulaQueue
    {
        private ConcurrentQueue<double[,]> queue;
        public CopulaQueue()
        {
            queue = new ConcurrentQueue<double[,]>();
        }
        public void Enqueue(double[,] matrix)
        {
            // insert a matrix into data structure
            queue.Enqueue(matrix);
        }
        public double[,] Dequeue()
        {
            // remove a matrix from data structure
            double[,] matrix = null;
            bool hasValue = false;
            while (!hasValue) hasValue = queue.TryDequeue(out matrix);
            return matrix;
        }
    }
    // ********************************************************************
    //
    // collection of methods for different types of statistical calculations
    public static class StatTools
    {
        // rational approximation for the inverse of standard normal cumulative distribution. 
        // the distribution has a mean of zero and a standard deviation of one.
        // source : Peter Acklam web page home.online.no/~pjacklam/notes/invnorm/
        public static double NormSInv(double x)
        {
            const double a1 = -39.6968302866538; const double a2 = 220.946098424521;
            const double a3 = -275.928510446969; const double a4 = 138.357751867269;
            const double a5 = -30.6647980661472; const double a6 = 2.50662827745924;
            //
            const double b1 = -54.4760987982241; const double b2 = 161.585836858041;
            const double b3 = -155.698979859887; const double b4 = 66.8013118877197;
            const double b5 = -13.2806815528857;
            //
            const double c1 = -7.78489400243029E-03; const double c2 = -0.322396458041136;
            const double c3 = -2.40075827716184; const double c4 = -2.54973253934373;
            const double c5 = 4.37466414146497; const double c6 = 2.93816398269878;
            //
            const double d1 = 7.78469570904146E-03; const double d2 = 0.32246712907004;
            const double d3 = 2.445134137143; const double d4 = 3.75440866190742;
            //
            const double p_low = 0.02425; const double p_high = 1.0 - p_low;
            double q = 0.0; double r = 0.0; double c = 0.0;
            //
            if ((x > 0.0) && (x < 1.0))
            {
                if (x < p_low)
                {
                    // rational approximation for lower region
                    q = Math.Sqrt(-2.0 * Math.Log(x));
                    c = (((((c1 * q + c2) * q + c3) * q + c4) * q + c5) * q + c6) / ((((d1 * q + d2) * q + d3) * q + d4) * q + 1);
                }
                if ((x >= p_low) && (x <= p_high))
                {
                    // rational approximation for middle region
                    q = x - 0.5; r = q * q;
                    c = (((((a1 * r + a2) * r + a3) * r + a4) * r + a5) * r + a6) * q / (((((b1 * r + b2) * r + b3) * r + b4) * r + b5) * r + 1);
                }
                if (x > p_high)
                {
                    // rational approximation for upper region
                    q = Math.Sqrt(-2 * Math.Log(1 - x));
                    c = -(((((c1 * q + c2) * q + c3) * q + c4) * q + c5) * q + c6) / ((((d1 * q + d2) * q + d3) * q + d4) * q + 1);
                }
            }
            else
            {
                // throw if given x value is out of bounds (less or equal to 0.0, greater or equal to 1.0) 
                throw new Exception("input parameter out of bounds");
            }
            return c;
        }
        public static double NormSDist(double x)
        {
            // returns the standard normal cumulative distribution function. 
            // the distribution has a mean of zero and a standard deviation of one.
            double sign = 1.0;
            if (x < 0) sign = -1.0;
            return 0.5 * (1.0 + sign * errorFunction(Math.Abs(x) / Math.Sqrt(2.0)));
        }
        private static double errorFunction(double x)
        {
            // uses Hohner's method for improved efficiency.
            const double a1 = 0.254829592; const double a2 = -0.284496736;
            const double a3 = 1.421413741; const double a4 = -1.453152027;
            const double a5 = 1.061405429; const double a6 = 0.3275911;
            x = Math.Abs(x); double t = 1 / (1 + a6 * x);
            return 1 - ((((((a5 * t + a4) * t) + a3) * t + a2) * t) + a1) * t * Math.Exp(-1 * x * x);
        }
    }
    // ********************************************************************
    //
    // collection of methods for different types of matrix operations
    public static class MatrixTools
    {
        public static double[,] Transpose(double[,] matrix)
        {
            // method for transposing matrix
            double[,] result = new double[matrix.GetUpperBound(1) + 1, matrix.GetUpperBound(0) + 1];
            //
            for (int i = 0; i < matrix.GetUpperBound(0) + 1; i++)
            {
                for (int j = 0; j < matrix.GetUpperBound(1) + 1; j++)
                {
                    result[j, i] = matrix[i, j];
                }
            }
            return result;
        }
        public static double[,] Multiplication(double[,] matrix1, double[,] matrix2)
        {
            // method for matrix multiplication
            double[,] result = new double[matrix1.GetUpperBound(0) + 1, matrix2.GetUpperBound(1) + 1];
            double v = 0.0;
            //
            for (int i = 0; i < matrix1.GetUpperBound(0) + 1; i++)
            {
                for (int j = 0; j < matrix2.GetUpperBound(1) + 1; j++)
                {
                    v = 0.0;
                    for (int k = 0; k < matrix1.GetUpperBound(1) + 1; k++)
                    {
                        v += matrix1[i, k] * matrix2[k, j];
                    }
                    result[i, j] = v;
                }
            }
            return result;
        }
    }
}

TEST RUN

When running the program, I get the following console printout. The printout shows, how our four consumers used in the example program are Dequeueing correlated 1x5 random matrices from CopulaQueue in parallel.

EFFICIENCY AND CORRELATION

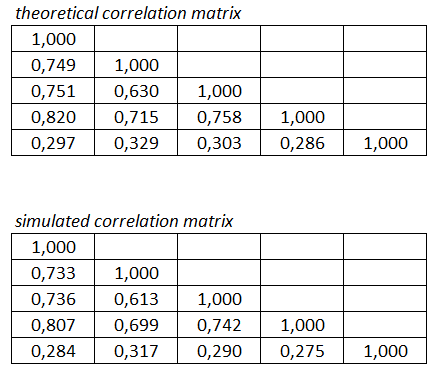
One million rows for 5x5 correlation matrix was processed 100 times, when testing efficiency of the producer part of the program. More specifically, four producers (CopulaEngine) are creating 1x5 matrices, consisting of five correlated uniformly distributed random numbers one by one and then sending these matrices to ConcurrentQueue wrapped in CopulaQueue class in parallel. Each of the four producers are then performing this operation 250 thousand times. Finally, the whole operation was repeated 1 hundred times and time elapsed for each repetition was saved for further analysis. The results of this experiment are reported in the table below.

As we can see in the table, multi-threading is nicely reducing processing time, but in a non-linear fashion. Next, I printed out one batch of correlated random numbers (1000000x5 matrix) into text file and compared theoretical and simulated correlation in Excel. Results are reported in the table below. We can see, that simulated correlation is in line with theoretical correlation (enough, IMHO).

READING REFERENCES

For me personally, the following two books are standing in their own class. Ben and Joseph Albahari C# in a nutshell is presenting pretty much everything one has to know (and a lot more) about C# and especially on .NET framework. Very nice thing is also, that Albahari brothers have been kindly offering a free chapter on multi-threading from this book on their website. Daniel Duffy and Andrea Germani C# for financial markets is presenting how to apply C# in financial programs. There are a lot of extremely useful examples on multi-threaded programs, especially on using multi-threading in Monte Carlo applications and the general usage of Producer-Consumer pattern, when using multi-threading.

Again, Big thanks for reading my blog and Happy and Better New Year 2015 for everybody.

-Mike

Write/read dynamic matrix between Excel and C# with Excel-DNA

This time I wanted to share some quick technical information about how to write or read dynamic matrix between Excel and C# program with Excel-DNA. The scheme what I am presenting here, applies to the case in which we use Excel as input/output platform for some C# program. By saying dynamic matrix, I am referring to the case, in which the dimensions of the input or output matrix are not known at compile time.

To make the long story shorter, you can use the existing program already presented in this blog posting as a base for this new example program. Just replace the content of ExcelInterface.cs file with the information given below.

C# PROGRAM

using System;
using ExcelDna.Integration;
using System.Windows.Forms;
//
namespace ExcelInterface
{
    public static class ExcelInterface
    {
        private static dynamic Excel;
        //
        public static void execute()
        {
            try
            {
                // Create Excel application and random number generator
                Excel = ExcelDnaUtil.Application;
                Random random = new Random(Guid.NewGuid().GetHashCode());
                //
                //
                //
                // CASE 1 : WRITE DYNAMIC MATRIX TO EXCEL
                int rows = (int)Excel.Range("_rows").Value2;
                int cols = (int)Excel.Range("_cols").Value2;
                double[,] matrix = new double[rows, cols];
                //
                // fill matrix with random numbers
                for (int i = 0; i < rows; i++)
                {
                    for (int j = 0; j < cols; j++)
                    {
                        matrix[i, j] = random.NextDouble();
                    }
                }
                // clear old data from output range by using Range.CurrentRegion property
                Excel.Range["_output"].CurrentRegion = "";
                //
                // resize output range to match with the dimensions of newly created random matrix
                Excel.Range["_output"].Resize[rows, cols] = matrix;
                //
                //
                //
                // CASE 2 : READ DYNAMIC MATRIX FROM EXCEL
                object[,] input = (object[,])Excel.Range["_output"].CurrentRegion.Value2;
                rows = input.GetUpperBound(0);
                cols = input.GetUpperBound(1);
                double sum = 0.0;
                //
                // sum all matrix items, calculate average and write it back to Excel
                foreach (object item in input) sum += (double)item;
                Excel.Range["_average"] = (sum / (rows * cols));
            }
            catch (Exception e)
            {
                MessageBox.Show(e.Message.ToString());
            }
        }
    }
}

In a nutshell, after creating ExcelDnaUtil.Application, we are able to use some extremely useful properties for manipulating Excel.Range object, such as CurrentRegion, Offset and Resize.

EXCEL WORKSHEET SETUPS

Dimensions for dynamic matrix output are given by the user in cells F4 and F5. Output matrix is printed to cell B8 (top left cell of output matrix). Input matrix is the same as output matrix and the C#-processed output (arithmetic average of all input matrix values) is printed into cell F6.

We have to set a couple of named Excel ranges for C# program. All the needed four named ranges are given in the screenshot below.

After implementing these range names, create a new button (Forms Controls) to this worksheet and put our C# program name into Macro box (execute). By doing this, we can get rid of the VBA code (Application.Run) completely. Any public static void method in our .NET code will be registered by Excel-DNA as a macro in Excel. Thanks for this tip to Govert Van Drimmelen (the inventor and author of Excel-DNA). After implementing all these steps, we are ready to use the program.

The purpose of this posting was to show how to handle dynamic data IO to/from Excel in C# program with Excel-DNA. For learning more things about Excel-DNA, check out its homepage. Getting more information and examples with your problems, the main source is Excel-DNA google group. Excel-DNA is an open-source project, and we (the happy users) can invest its future development by making a donation.

Thanks for reading my blog and happy waiting until Christmas.

-Mike