Discovering new tools for implementing numerical stuff is refreshing. This time, I wanted to present my calibration implementation for
SABR model in C# by using
Alglib numerical library. The thing I really like in Alglib, is its easiness of use : just find Alglib
download page,
download proper C# version, create a new C# project and add reference
to DLL file included in download folder - that's all. Like in my previous
post, optimization routine for this task has also been implemented by using
Levenberg-Marquardt algorithm.
FLYING CARPETS
Let us see the end product first. SABR coefficients have been calibrated for 16 different volatility skews. By using four calibrated parameters within SABR model, we should get extremely close replica of original volatility skew. Original forward volatility surface and its SABR-calibrated replica is presented in the screenshot below. Source data has been taken from
this great book (Excel files included) written by Richard Flavell. The essence of SABR model calibration has been chewed in the chapter 10.
SKEW DISSECTION
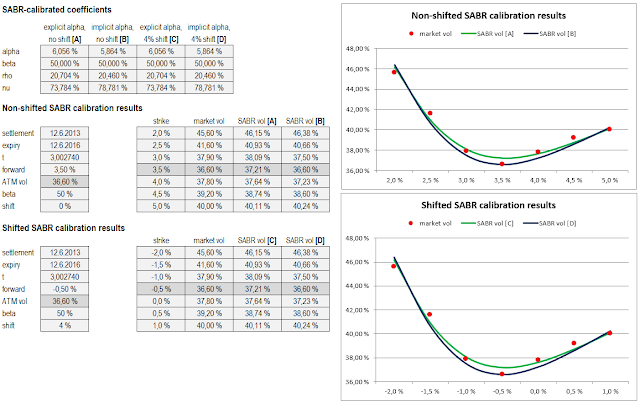
In order to validate this C# implementation, I have been replicating
example (Non-shifted SABR calibration results) found in MathWorks page on SABR model calibration. Original example data and calibration results of this C# implementation are presented in the screenshot below.
Additional results have been presented for
shifted SABR model calibrations. On the current low rate environment (in some currencies) we may enter into negative strike/forward rate territory. As this happens, log-normal model will crash. For such cases, using shifted log-normal SABR model is deceptively simple : constant shift will be added into strike prices and forward rates, in order to be able to calibrate the model.
It should be noted, that (in this implementation) beta coefficient is assumed to be a given estimated constant as this is usually a market practice. Moreover, the program is able to calibrate the model by solving three remaining coefficients (alpha, rho, nu) directly or then solving alpha implicitly from two remaining coefficients (rho, nu). These two calibration schemes have been presented in MathWorks
example (Method 1 and Method 2). Finally, calibration speed (this should not be a problem anyway) and especially accuracy can be greatly improved by using
Vector-Jacobian scheme (done in my previous post) and explicitly defined analytical partial derivatives instead of their numerical equivalents (finite difference).
THE PROGRAM
In order to test this calibration program, create a new C# project
(SABRCalibrationTester), copy-paste the following code into a new CS file and add
reference to Alglib DLL file.
using System;
using System.Collections.Generic;
using System.Linq;
namespace SABRCalibrationTester
{
class Program
{
static void Main(string[] args)
{
double beta = 0.5;
double expiry = 3.0027397260274;
double forward = 0.035;
double atmVolatility = 0.366;
double[] strike = new double[] { 0.02, 0.025, 0.03, 0.035, 0.04, 0.045, 0.05 };
double[] volatility = new double[] { 0.456, 0.416, 0.379, 0.366, 0.378, 0.392, 0.4 };
double[] coefficients = null;
//
// case 1 : use explicit alpha
// order of initial coefficients : alpha, rho, nu
SABR skew_3Y = new SABR(beta, expiry, forward, atmVolatility, strike, volatility);
coefficients = new double[] { 0.25, 0.25, 0.25 };
LevenbergMarquardtSolver.Solve(ref coefficients, 7, (IFunctionVector)skew_3Y);
Print(skew_3Y, "explicit alpha, no shift");
//
// case 2 : use implicit alpha
// order of initial coefficients : rho, nu
coefficients = new double[] { 0.25, 0.25 };
LevenbergMarquardtSolver.Solve(ref coefficients, 7, (IFunctionVector)skew_3Y);
Print(skew_3Y, "implicit alpha, no shift");
//
// case 3 : use explicit alpha and 4% shift factor
// order of initial coefficients : alpha, rho, nu
// create negative forward/strike scenario by shifting forward rate and strike prices down by 4%
forward = -0.005;
strike = new double[] { -0.02, -0.015, -0.01, -0.005, 0.0, 0.005, 0.01 };
double shift = 0.04;
SABR shiftedSkew_3Y = new SABR(beta, expiry, forward, atmVolatility, strike, volatility, shift);
coefficients = new double[] { 0.25, 0.25, 0.25 };
LevenbergMarquardtSolver.Solve(ref coefficients, 7, (IFunctionVector)shiftedSkew_3Y);
Print(shiftedSkew_3Y, "explicit alpha, 4% shift");
//
// case 4 : use implicit alpha and 4% shift factor
// order of initial coefficients : rho, nu
coefficients = new double[] { 0.25, 0.25 };
LevenbergMarquardtSolver.Solve(ref coefficients, 7, (IFunctionVector)shiftedSkew_3Y);
Print(shiftedSkew_3Y, "implicit alpha, 4% shift");
}
public static void Print(SABR sabr, string message)
{
// print message, SABR-calibrated coefficients and volatility skew
Console.WriteLine(message);
Console.WriteLine(String.Format("Alpha = {0:0.000%}", sabr.Alpha));
Console.WriteLine(String.Format("Beta = {0:0.000%}", sabr.Beta));
Console.WriteLine(String.Format("Rho = {0:0.000%}", sabr.Rho));
Console.WriteLine(String.Format("Nu = {0:0.000%}", sabr.Nu));
List<double> skew = sabr.SABRSkew().ToList<double>();
skew.ForEach(it => Console.WriteLine(String.Format("{0:0.000%}", it)));
Console.WriteLine();
}
}
//
//
//
//
/// <summary>
/// interface for function vector callback method, required by LevenbergMarquardtSolver class
/// </summary>
public interface IFunctionVector
{
void callback(double[] x, double[] fi, object obj);
}
//
/// <summary>
/// interface : definition for jacobian matrix callback method, optionally required by LevenbergMarquardtSolver class
/// </summary>
public interface IJacobianMatrix
{
void callback(double[] x, double[] fi, double[,] jac, object obj);
}
//
/// <summary>
/// static wrapper class for Alglib Levenberg-Marquardt solver implementation
/// </summary>
public static class LevenbergMarquardtSolver
{
// alglib report is exposed to public
public static alglib.minlmreport report;
private static alglib.minlmstate state;
//
/// <summary>
/// create LMA minimization solver using only function vector ('V' vector method)
/// </summary>
/// <param name="x">array of initial coefficients</param>
/// <param name="m">number of functions</param>
/// <param name="functionVector">IFunctionVector interface implementation</param>
public static void Solve(ref double[] x, int m, IFunctionVector functionVector,
// optional parameters which are set to default values
double diffstep = 1E-08, double epsg = 1E-15, double epsf = 0.0, double epsx = 0.0, int maxits = 0)
{
// create LM model, set termination conditions, perform optimization and get results
alglib.minlmcreatev(m, x, diffstep, out state);
alglib.minlmsetcond(state, epsg, epsf, epsx, maxits);
alglib.minlmoptimize(state, functionVector.callback, null, null);
alglib.minlmresults(state, out x, out report);
}
//
/// <summary>
/// create LMA minimization solver using function vector and Jacobian matrix ('VJ' vector-jacobian method)
/// </summary>
/// <param name="x">array of initial coefficients</param>
/// <param name="m">number of functions</param>
/// <param name="functionVector">IFunctionVector interface implementation</param>
/// <param name="jacobianMatrix">IJacobianMatrix interface implementation</param>
public static void Solve(ref double[] x, int m, IFunctionVector functionVector, IJacobianMatrix jacobianMatrix,
// optional parameters which are set to default values
double epsg = 1E-15, double epsf = 0.0, double epsx = 0.0, int maxits = 0)
{
// create LM model, set termination conditions, perform optimization and get results
alglib.minlmcreatevj(m, x, out state);
alglib.minlmsetcond(state, epsg, epsf, epsx, maxits);
alglib.minlmoptimize(state, functionVector.callback, jacobianMatrix.callback, null, null);
alglib.minlmresults(state, out x, out report);
}
}
//
//
//
//
/// <summary>
/// class calibrating SABR volatility skew for a given set of parameters
/// class implements IFunctionVector interface, uses static MathTools class
/// </summary>
public class SABR : IFunctionVector
{
// private member data
private double alpha;
private double beta;
private double rho;
private double nu;
private double expiry;
private double forward;
private double atmVolatility;
private double shift;
private double[] strike;
private double[] marketVolatility;
//
// public read-only access to SABR coefficients
public double Alpha { get { return this.alpha; } }
public double Beta { get { return this.beta; } }
public double Rho { get { return this.rho; } }
public double Nu { get { return this.nu; } }
public double Expiry { get { return this.expiry; } }
public double Forward { get { return this.forward; } }
public double ATMVolatility { get { return this.atmVolatility; } }
public double Shift { get { return this.shift; } }
public double[] Strike { get { return this.strike; } }
public double[] MarketVolatility { get { return this.marketVolatility; } }
//
/// <summary>
/// constructor
/// </summary>
/// <param name="beta">assumed to be a given constant within interval [0, 1]</param>
/// <param name="expiry">expiration time for forward</param>
/// <param name="forward">forward market quote</param>
/// <param name="atmVolatility">at-the-money market volatility quote</param>
/// <param name="strike">array of strike prices for corresponding market volatility quotes</param>
/// <param name="volatility">array of market volatility quotes</param>
public SABR(double beta, double expiry, double forward, double atmVolatility, double[] strike, double[] volatility, double shift = 0.0)
{
this.beta = beta;
this.expiry = expiry;
this.forward = forward;
this.atmVolatility = atmVolatility;
this.strike = strike;
this.marketVolatility = volatility;
this.shift = shift;
}
/// <summary>
/// retrieve array of SABR-calibrated volatilities
/// </summary>
public double[] SABRSkew()
{
double[] skew = new double[strike.Length];
for (int i = 0; i < skew.Length; i++)
{
skew[i] = explicitAlphaVolatility(forward + shift, strike[i] + shift, expiry, alpha, beta, nu, rho);
}
return skew;
}
/// <summary>
/// solve alpha coefficient
/// </summary>
private double solveForAlpha(double f, double t, double ATMVol, double beta, double nu, double rho)
{
double constant = -ATMVol * Math.Pow(f, (1 - beta));
double linear = 1.0 + (2.0 - 3.0 * Math.Pow(rho, 2.0)) / 24.0 * Math.Pow(nu, 2.0) * t;
double quadratic = 0.25 * rho * nu * beta * t / Math.Pow(f, (1.0 - beta));
double cubic = Math.Pow(1.0 - beta, 2.0) * t / (24.0 * Math.Pow(f, (2.0 - 2.0 * beta)));
//
double root = 0.0;
if (cubic > 0.0) root = MathTools.SmallestPositiveCubicRoot(cubic, quadratic, linear, constant);
if (cubic == 0.0) root = MathTools.SmallestPositiveQuadraticRoot(quadratic, linear, constant);
return root;
}
/// <summary>
/// calculate volatility with explicitly given alpha
/// </summary>
private double explicitAlphaVolatility(double f, double x, double t, double alpha, double beta, double nu, double rho)
{
double[] SABR = new double[3];
double sabrz, y;
//
// U-term
SABR[0] = alpha / (Math.Pow(f * x, (1.0 - beta) / 2.0))
* (1.0 + Math.Pow(1.0 - beta, 2.0) / 24.0 * Math.Pow(Math.Log(f / x), 2.0)
+ (Math.Pow(1.0 - beta, 4.0) / 1920.0) * Math.Pow(Math.Log(f / x), 4.0));
//
if (Math.Abs(f - x) > Math.Pow(10, -8.0))
{
sabrz = (nu / alpha) * Math.Pow(f * x, (1 - beta) / 2.0) * Math.Log(f / x);
y = (Math.Sqrt(1.0 - 2.0 * rho * sabrz + Math.Pow(sabrz, 2.0)) + sabrz - rho) / (1.0 - rho);
//
if (Math.Abs(y - 1.0) < Math.Pow(10, -8.0))
{
SABR[1] = 1.0;
}
else
{
if (y > 0.0)
{
SABR[1] = sabrz / Math.Log(y);
}
else
{
SABR[1] = 1.0;
}
}
}
else
{
SABR[1] = 1.0;
}
//
// V-term
SABR[2] = 1.0 + (((Math.Pow(1.0 - beta, 2.0) / 24.0) * (Math.Pow(alpha, 2.0) / (Math.Pow(f * x, 1.0 - beta))))
+ ((rho * beta * nu * alpha) / (4.0 * (Math.Pow(f * x, (1.0 - beta) / 2.0))))
+ ((((2.0 - 3.0 * Math.Pow(rho, 2.0)) / 24.0) * Math.Pow(nu, 2.0)))) * t;
//
return SABR[0] * SABR[1] * SABR[2];
}
/// <summary>
/// calculate volatility without explicitly given alpha
/// </summary>
private double implicitAlphaVolatility(double f, double x, double t, double vol, double beta, double nu, double rho)
{
this.alpha = solveForAlpha(f, t, vol, beta, nu, rho);
return explicitAlphaVolatility(f, x, t, alpha, beta, nu, rho);
}
/// <summary>
/// callback method for LMA solver in order to calculate vector of function values
/// </summary>
void IFunctionVector.callback(double[] x, double[] fi, object obj)
{
// calculate squared differences of SABR volatility and market volatility
// assign calculated squared differences into function vector fi
for (int i = 0; i < fi.Count(); i++)
{
double SABR_VOL = 0.0;
//
// solve for three coefficients : alpha = x[0], rho = x[1] and nu = x[2]
if (x.Count() == 3) SABR_VOL = explicitAlphaVolatility(forward + shift, strike[i] + shift, expiry, x[0], beta, x[2], x[1]);
//
// solve for two coefficients (alpha is implicitly solved) : rho = x[0] and nu = x[1]
if (x.Count() == 2) SABR_VOL = implicitAlphaVolatility(forward + shift, strike[i] + shift, expiry, atmVolatility, beta, x[1], x[0]);
fi[i] = Math.Pow(marketVolatility[i] - SABR_VOL, 2.0);
}
//
// update class member data coefficients
if (x.Count() == 3)
{
this.alpha = x[0];
this.rho = x[1];
this.nu = x[2];
}
else
{
this.rho = x[0];
this.nu = x[1];
this.alpha = solveForAlpha(forward + shift, expiry, atmVolatility, beta, this.nu, this.rho);
}
}
}
//
//
//
//
public static class MathTools
{
/// <summary>
/// find the smallest positive root for a given cubic polynomial function
/// </summary>
/// <param name="cubic">coefficient of cubic term</param>
/// <param name="quadratic">coefficient of quadratic term</param>
/// <param name="linear">coefficient of linear term</param>
/// <param name="constant">constant term</param>
public static double SmallestPositiveCubicRoot(double cubic, double quadratic, double linear, double constant)
{
double[] roots = new double[3];
double a, b, c, r, q, capA, capB, theta;
double root = 0.0;
//
a = quadratic / cubic;
b = linear / cubic;
c = constant / cubic;
q = (Math.Pow(a, 2.0) - 3.0 * b) / 9.0;
r = (2.0 * Math.Pow(a, 3.0) - 9.0 * a * b + 27.0 * c) / 54.0;
//
if ((Math.Pow(r, 2.0) - Math.Pow(q, 3.0)) >= 0.0)
{
capA = -Math.Sign(r) * Math.Pow(Math.Abs(r) + Math.Sqrt(Math.Pow(r, 2.0) - Math.Pow(q, 3.0)), (1.0 / 3.0));
if (capA == 0.0)
{
capB = 0.0;
}
else
{
capB = q / capA;
}
root = capA + capB - a / 3.0;
}
else
{
theta = Math.Acos(r / Math.Pow(q, 1.5));
//
// three available roots
roots[0] = -2.0 * Math.Sqrt(q) * Math.Cos(theta / 3.0) - a / 3.0;
roots[1] = -2.0 * Math.Sqrt(q) * Math.Cos(theta / 3.0 + 2.0943951023932) - a / 3.0;
roots[2] = -2.0 * Math.Sqrt(q) * Math.Cos(theta / 3.0 - 2.0943951023932) - a / 3.0;
//
// identify the smallest positive root
if (roots[0] > 0.0) root = roots[0];
if (roots[1] > 0.0) root = roots[1];
if (roots[2] > 0.0) root = roots[2];
if (roots[1] > 0.0 && roots[1] < root) root = roots[1];
if (roots[2] > 0.0 && roots[2] < root) root = roots[2];
}
return root;
}
//
/// <summary>
/// find the smallest positive root for a given quadratic polynomial function
/// throws exception in the case of finding complex roots
/// </summary>
/// <param name="quadratic">coefficient of quadratic term</param>
/// <param name="linear">coefficient of linear term</param>
/// <param name="constant">constant term</param>
public static double SmallestPositiveQuadraticRoot(double quadratic, double linear, double constant)
{
double x1, x2;
double root = 0.0;
double discriminant = Math.Pow(linear, 2.0) - 4.0 * quadratic * constant;
//
// case : complex roots (throw exception)
if (discriminant < 0.0) throw new Exception("No real roots available");
//
// case : one real root
if (discriminant == 0.0) root = -linear / (2.0 * quadratic);
//
// case : two real roots
if (discriminant > 0.0)
{
x1 = (-linear + Math.Sqrt(discriminant)) / (2.0 * quadratic);
x2 = (-linear - Math.Sqrt(discriminant)) / (2.0 * quadratic);
root = x1;
if ((x2 < x1) && (x2 > 0.0)) root = x2;
}
return root;
}
}
}
Finally, thanks for reading my blog.
-Mike