IMPLIED SURVIVAL PROBABILITY
Calculating implied survival probabilities from CDS prices follows the same idea, as calculating implied volatility from option price. For options, we have known market price, from which we can numerically solve the corresponding option volatility by using option pricing model. For CDS, we have known market price, from which we can solve the corresponding survival probability by using CDS pricing model. This is exactly the procedure, what this algorithm is doing. However, instead of just calculating one survival probability for a given CDS price, the algorithm is calculating all survival probabilities for a given CDS term structure. The pricing model for CDS is standard model (JP Morgan approach).Update (9.11.2016) : This presented implementation (using simple JP Morgan CDS model) ignores the effect of premium leg accruals. The resulting bias is relatively insignificant for low CDS levels but becomes material with high CDS levels. The issue has been chewed in the paper published by Lehman Brothers Fixed Income Quantitative Credit Research (Dominic O'Kane, Stuart Turnbull). On chapter 5, there is a discussion concerning premium leg valuation and related accrual effects. There is also a suggestion available for including premium accrual into this CDS pricing model. Thanks for attentive blog visitor for outlining this issue.
FUNCTION INPUT/OUTPUT
Zero-coupon bond prices, CDS prices and recovery rate assumption are needed as market data input for calculations. VBA function survivalProbability takes market information matrix (curves) and recovery rate assumption value (recovery) as input parameters. Function then returns an array of survival probabilities. Default probabilities can then be calculated from survival probabilities.Input market information matrix (N x 3) should contain the following data in the following order:
- 1st row vector - maturities in years
- 2nd row vector - zero-coupon bond prices (ex. 0.9825)
- 3rd row vector - CDS prices as basis points (ex. 0.25 % is given as 25)
After giving required input parameters for this function and selecting correct range for function output, remember to press CTRL+SHIFT+ENTER for retrieving result array (N x 1) into worksheet.
VBA FUNCTION
Option Explicit ' ' function takes market curves matrix (Nx3) and recovery rate (1x1) as arguments, then calculates and ' returns vector of survival probabilities (Nx1) for a given market data ' matrix input data order: 1st row vector = time, 2nd row vector = zero-coupon bond prices, ' 3rd row vector = cds rates in basis points Public Function survivalProbability(ByRef curves As Range, ByVal recovery As Double) As Variant ' ' information for dimensioning arrays Dim nColumns As Integer: nColumns = curves.Columns.Count Dim nRows As Integer: nRows = curves.Rows.Count ' ' create arrays for data Dim p() As Double: ReDim p(0 To nRows) Dim c() As Double: ReDim c(0 To curves.Rows.Count, 1 To curves.Columns.Count) ' ' copy variant array data into new array, having 1 additional item for today c(0, 1) = 0: c(0, 2) = 1: c(0, 3) = 0 Dim cInput As Variant: cInput = curves.Value2 ' Dim i As Integer, j As Integer, k As Integer For i = 1 To nRows c(i, 1) = cInput(i, 1) c(i, 2) = cInput(i, 2) c(i, 3) = cInput(i, 3) Next i ' ' calculation of survival probabilities (SP) Dim L As Double: L = (1 - recovery) Dim term As Double, terms As Double, divider As Double, term1 As Double, term2 As Double ' For i = LBound(p) To UBound(p) ' If (i = 0) Then p(i) = 1# ' SP today is one If (i = 1) Then p(i) = L / ((c(i, 3) / 10000) * (c(i, 1) - c(i - 1, 1)) + L) ' first SP formula ' If (i > 1) Then ' SP after first period are calculated recursively terms = 0 For j = 1 To (i - 1) term = c(j, 2) * (L * p(j - 1) - (L + (c(j, 1) - c(j - 1, 1)) * (c(i, 3) / 10000)) * p(j)) terms = terms + term Next j ' divider = c(i, 2) * (L + (c(i, 1) - c(i - 1, 1)) * (c(i, 3) / 10000)) term1 = terms / divider term2 = (p(i - 1) * L) / (L + (c(i, 1) - c(i - 1, 1)) * (c(i, 3) / 10000)) p(i) = term1 + term2 End If Next i ' ' create output array excluding the first SP (for today) Dim result() As Double: ReDim result(1 To UBound(p)) For i = 1 To UBound(p) result(i) = p(i) Next i ' ' finally, transpose output array (Nx1) survivalProbability = Application.WorksheetFunction.Transpose(result) End Function '
CALCULATION EXAMPLE
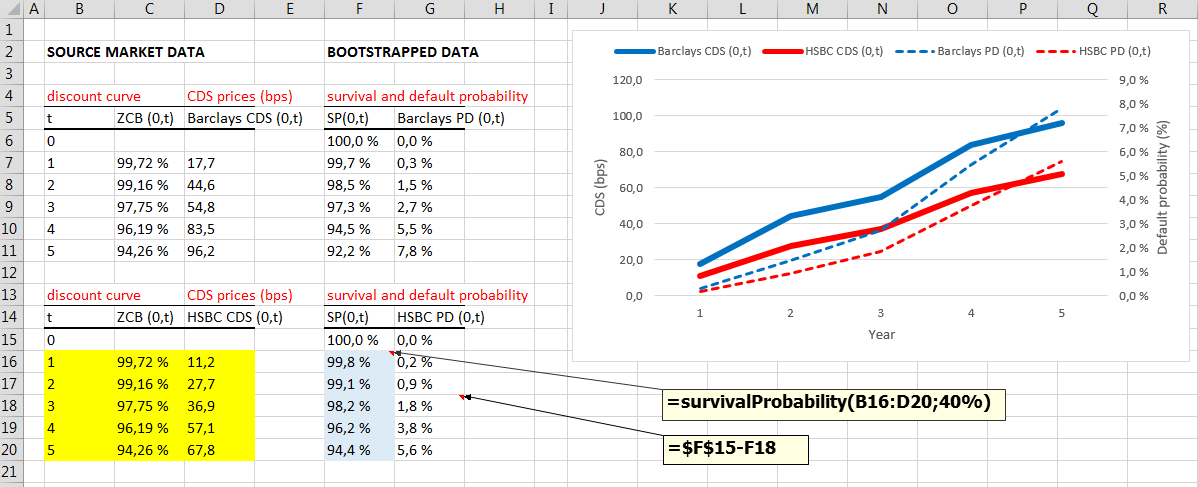
The following Excel screenshot presents the calculation of default probabilities for Barclays and HSBC. Market data has been retrieved in early january 2014. VBA function input matrix (curves) has been marked with yellow color. Function output range has been marked with blue color. Default probability (PD) is calculated in column G.
Thanks for reading.
-Mike
Man, you have just saved my CQF module5 :). Was very low on time due to work issues.
ReplyDeleteGlad I was able to help you :)
ReplyDeleteThank you, you have an excellent blog.
ReplyDeleteRow and column vectors mix up :S
ReplyDeleteI come from a CS background, it's rare to see such clean VBA code. Congrats!
ReplyDeleteCould you tell which formulae have been used?
ReplyDeleteStandard CDS pricing model is used. Survival probability is usually input for this model, but here it is solved out by using pricing model since we know the actual CDS prices. Since we are solving n survival probabilities, we are using bootstrapping method. After some algebra applied to pricing model, you will end up with formulas used in the main loop of this function.
ReplyDeleteThanks for the code.
ReplyDeleteJust a quick questions can I use this to extend to simulate CDS spreads/ ZCB yields?
eg, lets say if I use HW or HJM to simulate the spreads/yields and then use boostraps to calculate hazard rates?
Thanks a lot..
Hi, thanks a lot for posting this code! Just to double check my understanding of this, looking at the code I see that on the recursive calculation of terms you fixed the CDS value at each tenor by using i instead of j --> c(i, 3)/10000. Conceptually what would it mean to use the CDS of each previous year in the recursive calculation, that is using j instead of i?
ReplyDeleteHi,
ReplyDeleteI'm newbie with VBA.
I got some error when I tried to used Function with the data in excel below:#VALUE
=survivalProbability(B16:D20;40%). I used CTRL+SHIFT+ENTER as wrote.
Can anybody help please ?
Thanks-Matt
I just replicated the data in Excel and retrieved correct survival probabilities. The program is working. I may dare to say, that you are most probably doing something incorrectly.
DeletesurvivalProbability(B16:D20,40%)
DeleteCan anyone explain the term, terms, divider used in the code?
ReplyDeleteterm, terms, divider, term1 and term2 are just temporary variables used to save some space and to make program a bit more readable.
DeleteI can´t get the function to work either - could you maybe put the excel sheet up for download somewhere ?
ReplyDeleteHi, I'm a bit confused:
ReplyDeleteDefault probability=CDS/Loss so Survival pb = (Loss-CDS)/Loss.
In your 1st time step code it seems you have Survival pb=Loss/(CDS+Loss).
Is there something I'm missing?
JP Morgan (standard) model for pricing credit default swaps says :
ReplyDeleteCDS premium leg PV = CDS[T] * SUM(DF[0,Ti] * SP[Ti] * dT)
CDS Default leg PV = (1 - R) * SUM(DF[0,Ti] * (SP[Ti-1] - SP[Ti]))
R, dT, CDS[T] and DF[0,T..] are known. SP[Ti] can be inferred from this known data by using CDS pricing formula recursively. Today (at T=0) SP must be 1. For the first period, equate default and premium leg. After some tedious algebra, we get SP[T1] = (1 - R) / ((1 - R) + CDS * dT), which you see in that code.
Hi, thanks for your quick answer!
ReplyDeleteI think what is missing in your Premium leg is the accrual of the CDS up to the date of default when there is a default.
In your framework defaults are yearly at year end so whether default happens or not, the CDS coupon is paid for that year.
To simplify let’s look at the 1 year case, writing premium=default:
CDS=(1-R)(1-SP) as opposed to CDS*SP=(1-R)(1-SP).
So SP=(1-R-CDS)/(1-R) instead of SP=(1-R)/(1-R+SP).
The difference is minute for small CDS but becomes more material with large CDS.
Let’s check our intuition with an example: Maturity=1yr, if R=80% and CDS=20% then the probability of survival should be 0 (because the CDS is equal to the loss given default).
With my formula I get: SP=0/20%=0% with yours I get SP=20%/40%=50%.
This is why I was confused by some of the results initially and reached out.
I think because your defaults are annual year end you can in the general case replace SP[Ti] by SP[Ti-1] in your formula or else just add the accrual element in the case of default. But please check.
Princeton website has: ΣD(ti )q(ti )Sd + ΣD(ti ){q(ti-1 )-q(ti )}S*di /2 (because they have the default happen in the middle of the period).
https://www.princeton.edu/~markus/teaching/Eco467/10Lecture/CDS%20Presentation%20with%20References.pdf
I checked that Princeton paper and you are absolutely correct, that this presented equation (which is SIMPLE JP Morgan model) completely ignores the effect of such premium accruals, as you presented.
ReplyDeleteCheck out this paper: Lehman Brothers Fixed Income Quantitative Credit Research, (Dominic O'Kane and Stuart Turnbull). On chapter 5, there is a discussion concerning premium leg valuation and related accrual effects (the difference is minute for small CDS but becomes more material with large CDS): http://www.javaquant.net/papers/ValuationCDSLehman.pdf
There is also suggestions available for including such premium accrual into this model.
-Mike
Personally I have to admit, that I actually did not pay enough attention to this issue as I was writing that bootstrapping function. The devil is always in the details :)
Delete-Mike
No problem, I really appreciate your feedback. I am a trader not a quant, but I am working on a stochastic model where I used your code. I enjoy the constructive discussion! :)
ReplyDeleteIs it possible to compile this on CS.Lite of Bloomberg terminal?
ReplyDeleteCould you open up this question on a bit more detailed level?
DeleteHi Mikael,
ReplyDeleteI need to calculate PD e SP for not quoted counterparty. I researched this and suggested the implementation of a model with "sum" of different CDS (Country, Industry etc ...). Do you have any ideia about this model? Could you please provide me paper or something like that.
Thanks you.
Thank you
ReplyDeleteHi, thanks for this! Do you still recommend this approach?
ReplyDelete