Pricing equity basket option with Monte Carlo in VBA

Within the last three postings, I have been chewing the creation of correlated random numbers with Gaussian Copula model and some efficiency issues, when handling large matrices in VBA. This post is finally presenting some real-world application for these issues by pricing equity basket option with Monte Carlo method in VBA.

EQUITY BASKET OPTION
A basket option is an option where the payout is related to the cumulative performance of a specified basket of underlying assets. Typically examples include options on baskets of currencies and equities. In this option, the multifactor element is the multiple underlying assets incorporated into option structure. The payoff of single option is based on the value at expiry or exercise value of individual asset. In contrast, the payoff of basket option is based on the aggregate value of basket of assets.

There are analytical pricing formulas available for basket options, but in this example we will use Monte Carlo method for pricing. Pricing procedure for M assets and N simulations can be described with the following steps

1. Create matrix (NxM) of correlated normal random numbers by using Gaussian Copula
2. Simulate M asset paths by using standard Geometric Brownian Motion (GBM)
3. Sum all M simulated asset prices at expiration to get aggregate asset value at expiration
4. Calculate option payoff for aggregate asset value at expiration
5. Discount calculated payoff back to today
6. Repeat steps 2-5 N times
7. Calculate average for all discounted payoffs to get the option value today

For the structure presented in this example, the strike price is calculated as the sum of observed spot prices today.

PROGRAM DESIGN
We are aiming to have as flexible design as possible. This means, that first we try to identify the main components what might change in the future. The current design is presented in the picture below.





















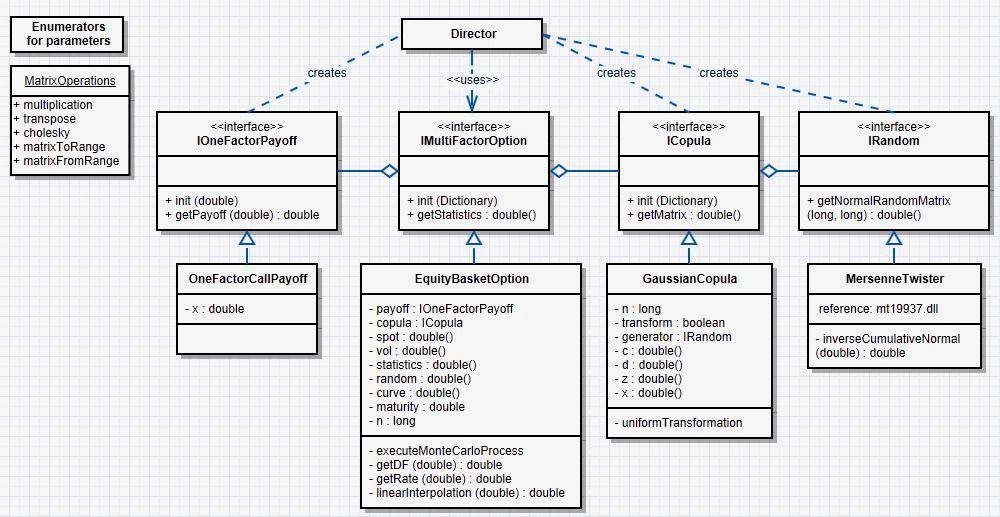
We can identify at least four important components, which we might want to change in the future.

1. Payoff - even we are pricing multifactor option, the payoff itself is one-factor payoff since we are calculating the difference of aggregate asset value at expiration and the strike price. In the future, we might want to create implementations for other types of payoffs. As the other parts of the program are communicating with payoff interface, it is easy to change the payoff type without having any modifications for other parts of the program.
2. Copula - in the future, we might want to create implementations for other types of copula models.
3. Random - in the future, we might want to create implementations for other types of random number generators.
4. Option - this example is pricing equity basket option, but it is also an implementation of multi-factor option interface. In the future, we might want to create implementations for other types of multi-factor options, such as the best-of or worst-of basket options. 

With this flexibility in our hands, we are already able to create pricers for many different types of multi-factor options with this proposed design. There are also some other small functionalities, which we might also have isolated behind separate interfaces, like Stochastic differential equation used (GBM) and handling interest rates and discount factors.

EXCEL INTERFACE
Input parameters for the program are read from Excel worksheet. The screenshot of interface is shown in the picture below.

Important input parameters are marked with yellow color. The program is configured to read all required input parameters from the following named Excel ranges.

1. Correlation matrix - range("F5:N13") = "_correlation"
2. Spot prices - range("P5:P13") = "_spot"
3. Spot voltilities - range("Q5:Q13") = "_vol"
4. Discount curve - range("T5:U19") = "_curve"
5. Number of simulations - range("C18") = "_simulations"
6. Maturity - range("C20") = "_maturity"
7. Error reporting - range("C21") = "_status"
8. Results reporting - range("C25") = "_result"

Random number generator type (Mersenne Twister) has been hard-coded inside the main program. The pink area in the picture is the correlation matrix override region. Correlations in the yellow area are coming directly from bloomberg (like the other market data), but can be overriden with values from override matrix, if needed. This is useful feature to have, if we want to investigate the effect of correlation between the assets on option values.

Note, that the number of assets in the basket is not hard-coded in anywhere. There is not any particular limitation for having exactly those nine stocks in the basket. When the parameters are created for the actual program, Copula implementation is creating its random number matrix based on the dimensions of given correlation matrix and the number of simulations. If we define the named Excel range for correlation to be (3 x 3) matrix and the number of simulations to be 250 000, Copula creates (250 000 x 3) matrix of correlated random numbers. This means, that the actual simulation procedure is then having total of 250 000 paths for each asset. The only requirement is, that the number of rows and columns of correlation matrix must be correspond to the number of rows in spot and volatility ranges.

THE PROGRAM
Copy-paste the following program and break it up into different VBA modules and classes. Follow the instructions given. For external library needed (dll), check my post on Gaussian Copula. Remember also to create reference into Microsoft Scripting Runtime library. Also, insert one ActiveX command button into pricer worksheet, name it as "btnExecute" and create event as shown below. The program starts, as we press this button.

' VBA worksheet (name = pricer)
Option Explicit
'
Private Sub btnExecute_Click()
    '
    On Error GoTo errorhandler: Range("_status") = ""
    '
    ' create parameter wrapper for copula
    Dim p_copula As New Scripting.Dictionary
    '
    ' add parameters for copula wrapper
    Dim correlation() As Double: correlation = MatrixOperations.matrixFromRange(Range("_correlation"))
    p_copula.Add P_CORRELATION_MATRIX, correlation
    p_copula.Add P_SIMULATIONS, CLng(Range("_simulations").value)
    p_copula.Add P_GENERATOR_TYPE, New MersenneTwister ' HARD-CODED !!
    p_copula.Add P_TRANSFORM_TO_UNIFORM, CBool("FALSE") ' HARD-CODED !!
    '
    ' create copula implementation and feed wrapper into it
    Dim copula As ICopula: Set copula = New GaussianCopula
    copula.init p_copula
    '
    '
    ' create parameter wrapper for multifactor option
    Dim p_option As New Scripting.Dictionary
    '
    ' add parameters for multifactor option wrapper
    p_option.Add P_COPULA_MODEL, copula
    p_option.Add P_SIMULATIONS, CLng(Range("_simulations").value)
    p_option.Add P_MATURITY, CDbl(Range("_maturity"))
    '
    Dim curve() As Double: curve = MatrixOperations.matrixFromRange(Range("_curve"))
    p_option.Add P_ZERO_CURVE, curve
    '
    Dim spot() As Double: spot = MatrixOperations.matrixFromRange(Range("_spot"))
    p_option.Add P_SPOT, spot
    '
    Dim vol() As Double: vol = MatrixOperations.matrixFromRange(Range("_vol"))
    p_option.Add P_VOLATILITY, vol
    '
    ' calculate basket strike price (assuming equal weights)
    Dim i As Long, strike As Double
    For i = 1 To UBound(spot)
        strike = strike + spot(i, 1)
    Next i
    '
    ' create payoff implementation and feed strike into it
    Dim payoff As IOneFactorPayoff: Set payoff = New OneFactorCallPayoff
    payoff.init strike
    p_option.Add P_PAYOFF, payoff
    '
    '
    ' create equity basket option and feed wrapper into it
    Dim basketOption As IMultiFactorOption: Set basketOption = New EquityBasketOption
    basketOption.init p_option
    '
    ' receive and write calculation results into Excel worksheet
    Dim result() As Double: result = basketOption.getStatistics()
    MatrixOperations.matrixToRange result, Range("_result")
    Exit Sub
    '
errorhandler:
    Range("_status") = Err.Description
End Sub
'
'
'
'
' standard VBA module (name = Enumerators)
Option Explicit
'
Public Enum E_
    P_CORRELATION_MATRIX = 1
    P_SPOT = 2
    P_VOLATILITY = 3
    P_ZERO_CURVE = 4
    P_SIMULATIONS = 5
    P_GENERATOR_TYPE = 6
    P_MATURITY = 7
    P_COPULA_MODEL = 8
    P_TRANSFORM_TO_UNIFORM = 9
    P_PAYOFF = 10
    P_STRIKE = 11
End Enum
'
'
'
'
' standard VBA module (name = MatrixOperations)
Option Explicit
'
Public Function multiplication(ByRef m1() As Double, ByRef m2() As Double) As Double()
    '
    ' get matrix multiplication
    Dim result() As Double: ReDim result(1 To UBound(m1, 1), 1 To UBound(m2, 2))
    Dim i As Long, j As Long, k As Long
    '
    Dim r1 As Long: r1 = UBound(m1, 1)
    Dim c1 As Long: c1 = UBound(m1, 2)
    Dim r2 As Long: r2 = UBound(m2, 1)
    Dim c2 As Long: c2 = UBound(m2, 2)
    Dim v As Double
    '
    For i = 1 To r1
        For j = 1 To c2
            v = 0
            '
            For k = 1 To c1
                v = v + m1(i, k) * m2(k, j)
            Next k
            result(i, j) = v
        Next j
    Next i
    multiplication = result
End Function
'
Public Function transpose(ByRef m() As Double)
    '
    ' get matrix transpose
    Dim nRows As Long: nRows = UBound(m, 1)
    Dim nCols As Long: nCols = UBound(m, 2)
    Dim result() As Double: ReDim result(1 To nCols, 1 To nRows)
    '
    Dim i As Long, j As Long
    For i = 1 To nRows
        For j = 1 To nCols
            result(j, i) = m(i, j)
        Next j
    Next i
    transpose = result
End Function
'
Public Function cholesky(ByRef c() As Double) As Double()
    '
    ' create cholesky decomposition, a lower triangular matrix
    ' d = decomposition, c = correlation matrix
    Dim s As Double
    Dim n As Long: n = UBound(c, 1)
    Dim m As Long: m = UBound(c, 2)
    Dim d() As Double: ReDim d(1 To n, 1 To m)
    '
    Dim i As Long, j As Long, k As Long
    For j = 1 To n
        s = 0
        For k = 1 To j - 1
            s = s + d(j, k) ^ 2
        Next k
        d(j, j) = (c(j, j) - s)
        If (d(j, j) <= 0) Then Exit For
        '
        d(j, j) = Sqr(d(j, j))
        '
        For i = (j + 1) To n
            s = 0
            For k = 1 To (j - 1)
                s = s + d(i, k) * d(j, k)
            Next k
            d(i, j) = (c(i, j) - s) / d(j, j)
        Next i
    Next j
    cholesky = d
End Function
'
Public Function matrixToRange(ByRef m() As Double, ByRef r As Range)
    '
    ' write matrix into Excel range
    r.Resize(UBound(m, 1), UBound(m, 2)) = m
End Function
'
Public Function matrixFromRange(ByRef r As Range) As Double()
    '
    ' read matrix from Excel range
    Dim v As Variant: v = r.Value2
    Dim r_ As Long: r_ = UBound(v, 1)
    Dim c_ As Long: c_ = UBound(v, 2)
    Dim m() As Double: ReDim m(1 To r_, 1 To c_)
    '
    ' transform variant to double
    Dim i As Long, j As Long
    For i = 1 To r_
        For j = 1 To c_
            m(i, j) = CDbl(v(i, j))
        Next j
    Next i
    matrixFromRange = m
End Function
'
'
'
'
' VBA class module (name = ICopula)
Option Explicit
'
Public Function init(ByRef parameters As Scripting.Dictionary)
    ' interface - no implementation
End Function
'
Public Function getMatrix() As Double()
    ' interface - no implementation
End Function
'
'
'
'
' VBA class module (name = GaussianCopula)
Option Explicit
'
Implements ICopula
'
Private n As Long ' number of simulations
Private transform As Boolean ' condition for uniform transformation
Private generator As IRandom ' random number generator implementation
'
Private c() As Double ' correlation matrix
Private d() As Double ' cholesky decomposition matrix
Private z() As Double ' independent normal random variables
Private x() As Double ' correlated normal random variables
'
Private Function ICopula_init(ByRef parameters As Scripting.Dictionary)
    '
    ' initialize class data and objects
    n = parameters(P_SIMULATIONS)
    transform = parameters(P_TRANSFORM_TO_UNIFORM)
    Set generator = parameters(P_GENERATOR_TYPE)
    c = parameters(P_CORRELATION_MATRIX)
End Function
'
Private Function ICopula_getMatrix() As Double()
    '
    ' create matrix of independent normal random numbers
    ReDim z(1 To n, 1 To UBound(c, 2))
    z = generator.getNormalRandomMatrix(UBound(z, 1), UBound(z, 2))
    '
    ' create cholesky decomposition
    d = MatrixOperations.cholesky(c)
    '
    ' create correlated normal random numbers
    z = MatrixOperations.transpose(z)
    x = MatrixOperations.multiplication(d, z)
    x = MatrixOperations.transpose(x)
    '
    ' transform correlated normal random numbers
    ' into correlated uniform random numbers
    If (transform) Then uniformTransformation
    ICopula_getMatrix = x
End Function
'
Private Function uniformTransformation()
    '
    ' map normal random number to uniform plane
    Dim nRows As Long: nRows = UBound(x, 1)
    Dim nCols As Long: nCols = UBound(x, 2)
    '
    Dim i As Long, j As Long
    For i = 1 To nRows
        For j = 1 To nCols
            x(i, j) = WorksheetFunction.NormSDist(x(i, j))
        Next j
    Next i
End Function
'
'
'
'
' VBA class module (name = IRandom)
Option Explicit
'
Public Function getNormalRandomMatrix( _
    ByVal nRows As Long, _
    ByVal nCols As Long) As Double()
    '
    ' interface - no implementation
    ' takes in two parameters (number of rows and columns) and
    ' returns double() filled with normal random variates
End Function
'
'
'
'
' VBA class module (name = MersenneTwister)
Option Explicit
'
Implements IRandom
'
Private Declare Function nextMT Lib "C:\temp\mt19937.dll" Alias "genrand" () As Double
'
Private Function IRandom_getNormalRandomMatrix( _
    ByVal nRows As Long, _
    ByVal nCols As Long) As Double()
    '
    ' retrieve NxM matrix with normal random numbers
    Dim r() As Double: ReDim r(1 To nRows, 1 To nCols)
    Dim i As Long, j As Long
    For i = 1 To nRows
        For j = 1 To nCols
            r(i, j) = InverseCumulativeNormal(nextMT())
        Next j
    Next i
    '
    IRandom_getNormalRandomMatrix = r
End Function
'
Public Function InverseCumulativeNormal(ByVal p As Double) As Double
    '
    ' Define coefficients in rational approximations
    Const a1 = -39.6968302866538
    Const a2 = 220.946098424521
    Const a3 = -275.928510446969
    Const a4 = 138.357751867269
    Const a5 = -30.6647980661472
    Const a6 = 2.50662827745924
    '
    Const b1 = -54.4760987982241
    Const b2 = 161.585836858041
    Const b3 = -155.698979859887
    Const b4 = 66.8013118877197
    Const b5 = -13.2806815528857
    '
    Const c1 = -7.78489400243029E-03
    Const c2 = -0.322396458041136
    Const c3 = -2.40075827716184
    Const c4 = -2.54973253934373
    Const c5 = 4.37466414146497
    Const c6 = 2.93816398269878
    '
    Const d1 = 7.78469570904146E-03
    Const d2 = 0.32246712907004
    Const d3 = 2.445134137143
    Const d4 = 3.75440866190742
    '
    'Define break-points
    Const p_low = 0.02425
    Const p_high = 1 - p_low
    '
    'Define work variables
    Dim q As Double, r As Double
    '
    'If argument out of bounds, raise error
    If p <= 0 Or p >= 1 Then Err.Raise 5
    '
    If p < p_low Then
        '
        'Rational approximation for lower region
        q = Sqr(-2 * Log(p))
        InverseCumulativeNormal = (((((c1 * q + c2) * q + c3) * q + c4) * q + c5) * q + c6) / _
        ((((d1 * q + d2) * q + d3) * q + d4) * q + 1)
        '
    ElseIf p <= p_high Then
        'Rational approximation for lower region
        q = p - 0.5
        r = q * q
        InverseCumulativeNormal = (((((a1 * r + a2) * r + a3) * r + a4) * r + a5) * r + a6) * q / _
        (((((b1 * r + b2) * r + b3) * r + b4) * r + b5) * r + 1)
        '
    ElseIf p < 1 Then
        'Rational approximation for upper region
        q = Sqr(-2 * Log(1 - p))
        InverseCumulativeNormal = -(((((c1 * q + c2) * q + c3) * q + c4) * q + c5) * q + c6) / _
        ((((d1 * q + d2) * q + d3) * q + d4) * q + 1)
    End If
End Function
'
'
'
'
' VBA class module (name = IOneFactorPayoff)
Option Explicit
'
Public Function init(ByVal x As Double)
    ' interface
End Function
'
Public Function getPayoff(ByVal s As Double) As Double
    ' interface
End Function
'
'
'
'
' VBA class module (name = OneFactorCallPayoff)
Option Explicit
'
Implements IOneFactorPayoff
'
Private x_ As Double
'
Private Function IOneFactorPayoff_getPayoff(ByVal s As Double) As Double
    IOneFactorPayoff_getPayoff = 0
    If (s > x_) Then IOneFactorPayoff_getPayoff = s - x_
End Function
'
Private Function IOneFactorPayoff_init(ByVal x As Double)
    x_ = x
End Function
'
'
'
'
' VBA class module (name = IMultiFactorOption)
Option Explicit
'
Public Function init(ByRef wrapper As Scripting.Dictionary)
    ' interface
End Function
'
Public Function getStatistics() As Double()
    ' interface
End Function
'
'
'
'
' VBA class module (name = EquityBasketOption)
Option Explicit
'
Private Declare Function GetTickCount Lib "kernel32.dll" () As Long
'
Implements IMultiFactorOption
'
Private payoff As IOneFactorPayoff
Private copula As ICopula
'
Private spot() As Double
Private vol() As Double
Private statistics() As Double
Private random() As Double
Private curve() As Double
'
Private maturity As Double
Private n As Long
Private startTime As Long
'
Private Function IMultiFactorOption_init(ByRef wrapper As Scripting.IDictionary)
    '
    ' extract objects and class member data from wrapper
    Set copula = wrapper(P_COPULA_MODEL)
    Set payoff = wrapper(P_PAYOFF)
    spot = wrapper(P_SPOT)
    vol = wrapper(P_VOLATILITY)
    curve = wrapper(P_ZERO_CURVE)
    n = wrapper(P_SIMULATIONS)
    maturity = wrapper(P_MATURITY)
End Function
'
Private Function IMultiFactorOption_getStatistics() As Double()
    '
    ' record start time
    startTime = GetTickCount()
    '
    ' get matrix of correlated normal random variates
    random = copula.getMatrix()
    '
    ' execute monte carlo and return results
    executeMonteCarloProcess
    IMultiFactorOption_getStatistics = statistics
End Function
'
Private Function executeMonteCarloProcess()
    '
    ' the actual monte carlo process
    Dim terminalValue() As Double: ReDim terminalValue(1 To n) ' container for all calculated payoffs
    Dim i As Long, j As Long, m As Long: m = UBound(spot)
    Dim r As Double: r = getRate(maturity) ' rate for risk-neutral drift
    Dim SDE As Double, drift As Double, noise As Double ' SDE process and its sub-components
    Dim value As Double
    '
    ' process random numbers
    For i = 1 To n
        value = 0
        '
        ' SDE process for m assets
        For j = 1 To m
            '
            ' since we have european option, we can create SDE process directly
            ' into maturity instead of simulating small time increments
            drift = (r - 0.5 * vol(j, 1) * vol(j, 1))
            noise = vol(j, 1) * Sqr(maturity) * random(i, j)
            SDE = spot(j, 1) * Exp(drift * maturity + noise)
            value = value + SDE
        Next j
        '
        ' push calculated basket payoffs into container
        terminalValue(i) = payoff.getPayoff(value)
    Next i
    '
    ' average and discount payoffs to get basket option value today
    Dim df As Double: df = getDF(maturity) ' zero-coupon bond price for discounting expectation
    Dim sum As Double, sumSq As Double
    For i = 1 To n
        value = terminalValue(i) * df
        sum = sum + value
        sumSq = sumSq + (value * value)
    Next i
    '
    ' HARD-CODED !!
    ' push statistics into result container (average, sample standard error, time elapsed)
    ReDim statistics(1 To 3, 1 To 1)
    statistics(1, 1) = (sum / n)
    statistics(2, 1) = Sqr((sumSq / n) - ((sum / n) * (sum / n))) / Sqr(n)
    statistics(3, 1) = ((GetTickCount - startTime) / 1000)
End Function
'
Private Function getDF(ByVal t As Double) As Double
    '
    ' calculate continuous-time discount factor
    Dim r As Double: r = linearInterpolation(t)
    getDF = Exp(-r * t)
End Function
'
Private Function getRate(ByVal t As Double) As Double
    '
    ' get zero-coupon bond yield
    getRate = linearInterpolation(t)
End Function
'
Private Function linearInterpolation(ByVal t As Double) As Double
    '
    ' get linear interpolation
    Dim n As Integer: n = UBound(curve, 1)
    Dim v As Double
    Dim i As Long
    '
    ' checking for boundaries
    If (t < curve(1, 1)) Then v = curve(1, 2): GoTo exitPoint
    If (t > curve(UBound(curve, 1), 1)) Then v = curve(UBound(curve, 1), 2): GoTo exitPoint
    '
    For i = 1 To (n - 1)
        If (t >= curve(i, 1)) And (t <= curve(i + 1, 1)) Then
            v = curve(i, 2) + (curve(i + 1, 2) - curve(i, 2)) * ((t - curve(i, 1)) / (curve(i + 1, 1) - curve(i, 1)))
            Exit For
        End If
    Next i
    '
exitPoint:
    linearInterpolation = v
End Function
'

PRICING RUN
In the testing run, equity basket has nine different GBP-nominated shares. Strike price has been calculated as the sum of current spot prices to be 12308.4 GBP. With the current correlation structure between the assets and 1.2 million simulated sample paths for each asset in the basket, the option value has been calculated to be approximately 631.8 GBP.

When changing all correlations to be exactly one with correlation override matrix, we get the value of 856.73 GBP, which should be approximately the same value as the sum of values of individually priced equity options. Plain Black & Scholes pricing model is giving the value of 856.32 GBP for such basket, so we are close enough.

Thanks for reading!

-Mike

Gaussian Copula implementation revisited

In my previous posting on matrix data structure, I compared the efficiency of processing matrix structures with different array data structures. The message was clear: two-dimensional arrays are the most efficient data structure when operating with large matrix operations. I have modified my implementation for Gaussian Copula in a such way, that it is using two-dimensional arrays instead of Matrix class.

Second version

The modified program is presented below. For required input data (Excel ranges), library references and external dll file, follow the instructions given on Gaussian Copula posting.

' standard VBA module (name = Enumerators)
Option Explicit
'
Public Enum E_
    P_SIMULATIONS = 1
    P_GENERATOR_TYPE = 2
    P_CORRELATION_MATRIX = 3
    P_TRANSFORM_TO_UNIFORM = 4
End Enum
'
'
'
' standard VBA module (name = MainProgram)
Option Explicit
'
Public Sub tester()
    '
    ' create correlation matrix object
    Dim correlation() As Double
    correlation = MatrixOperations.matrixFromRange(Sheets("Sheet1").Range("_correlation"))
    '
    ' create parameters for copula
    Dim parameters As New Scripting.Dictionary
    parameters.Add P_SIMULATIONS, CLng(Sheets("Sheet1").Range("_simulations").value)
    parameters.Add P_GENERATOR_TYPE, New MersenneTwister
    parameters.Add P_CORRELATION_MATRIX, correlation
    parameters.Add P_TRANSFORM_TO_UNIFORM, CBool(Sheets("Sheet1").Range("_transform").value)
    '
    ' create copula implementation
    Dim copula As ICopula: Set copula = New GaussianCopula
    copula.init parameters
    '
    ' get results from copula and write these into Excel
    Dim result() As Double: result = copula.getMatrix
    MatrixOperations.matrixToRange result, Sheets("Sheet1").Range("_dataDump")
    '
    ' release objects
    Set copula = Nothing
    Set parameters = Nothing
End Sub
'
'
'
' standard VBA module (name = MatrixOperations)
Option Explicit
'
Public Function multiplication(ByRef m1() As Double, ByRef m2() As Double) As Double()
    '
    ' get matrix multiplication
    Dim result() As Double: ReDim result(1 To UBound(m1, 1), 1 To UBound(m2, 2))
    Dim i As Long, j As Long, k As Long
    '
    Dim r1 As Long: r1 = UBound(m1, 1)
    Dim c1 As Long: c1 = UBound(m1, 2)
    Dim r2 As Long: r2 = UBound(m2, 1)
    Dim c2 As Long: c2 = UBound(m2, 2)
    Dim v As Double
    '
    For i = 1 To r1
        For j = 1 To c2
            v = 0
            '
            For k = 1 To c1
                v = v + m1(i, k) * m2(k, j)
            Next k
            result(i, j) = v
        Next j
    Next i
    multiplication = result
End Function
'
Public Function transpose(ByRef m() As Double)
    '
    ' get matrix transpose
    Dim nRows As Long: nRows = UBound(m, 1)
    Dim nCols As Long: nCols = UBound(m, 2)
    Dim result() As Double: ReDim result(1 To nCols, 1 To nRows)
    '
    Dim i As Long, j As Long
    For i = 1 To nRows
        For j = 1 To nCols
            result(j, i) = m(i, j)
        Next j
    Next i
    transpose = result
End Function
'
Public Function cholesky(ByRef c() As Double) As Double()
    '
    ' create cholesky decomposition, a lower triangular matrix
    ' d = decomposition, c = correlation matrix
    Dim s As Double
    Dim n As Long: n = UBound(c, 1)
    Dim m As Long: m = UBound(c, 2)
    Dim d() As Double: ReDim d(1 To n, 1 To m)
    '
    Dim i As Long, j As Long, k As Long
    For j = 1 To n
        s = 0
        For k = 1 To j - 1
            s = s + d(j, k) ^ 2
        Next k
        d(j, j) = (c(j, j) - s)
        If (d(j, j) <= 0) Then Exit For
        '
        d(j, j) = Sqr(d(j, j))
        '
        For i = (j + 1) To n
            s = 0
            For k = 1 To (j - 1)
                s = s + d(i, k) * d(j, k)
            Next k
            d(i, j) = (c(i, j) - s) / d(j, j)
        Next i
    Next j
    cholesky = d
End Function
'
Public Function matrixToRange(ByRef m() As Double, ByRef r As Range)
    '
    ' write matrix into Excel range
    r.Resize(UBound(m, 1), UBound(m, 2)) = m
End Function
'
Public Function matrixFromRange(ByRef r As Range) As Double()
    '
    ' read matrix from Excel range
    Dim v As Variant: v = r.Value2
    Dim r_ As Long: r_ = UBound(v, 1)
    Dim c_ As Long: c_ = UBound(v, 2)
    Dim m() As Double: ReDim m(1 To r_, 1 To c_)
    '
    ' transform variant to double
    Dim i As Long, j As Long
    For i = 1 To r_
        For j = 1 To c_
            m(i, j) = CDbl(v(i, j))
        Next j
    Next i
    matrixFromRange = m
End Function
'
'
'
' VBA class module (name = ICopula)
Option Explicit
'
' interface for copula model
'
Public Function init(ByRef parameters As Scripting.Dictionary)
    ' interface - no implementation
End Function
'
Public Function getMatrix() As Double()
    ' interface - no implementation
End Function
'
'
'
' VBA class module (name = GaussianCopula)
Option Explicit
'
Implements ICopula
'
Private n As Long ' number of simulations
Private transform As Boolean ' condition for uniform transformation
Private generator As IRandom ' random number generator implementation
'
Private c() As Double ' correlation matrix
Private d() As Double ' cholesky decomposition matrix
Private z() As Double ' independent normal random variables
Private x() As Double ' correlated normal random variables
'
Private Function ICopula_init(ByRef parameters As Scripting.Dictionary)
    '
    ' initialize class data and objects
    n = parameters(P_SIMULATIONS)
    transform = parameters(P_TRANSFORM_TO_UNIFORM)
    Set generator = parameters(P_GENERATOR_TYPE)
    c = parameters(P_CORRELATION_MATRIX)
End Function
'
Private Function ICopula_getMatrix() As Double()
    '
    ' create matrix of independent normal random numbers
    ReDim z(1 To n, 1 To UBound(c, 2))
    z = generator.getNormalRandomMatrix(UBound(z, 1), UBound(z, 2))
    '
    ' create cholesky decomposition
    d = MatrixOperations.cholesky(c)
    '
    ' create correlated normal random numbers
    z = MatrixOperations.transpose(z)
    x = MatrixOperations.multiplication(d, z)
    x = MatrixOperations.transpose(x)
    '
    ' transform correlated normal random numbers
    ' into correlated uniform random numbers
    If (transform) Then uniformTransformation
    ICopula_getMatrix = x
End Function
'
Private Function uniformTransformation()
    '
    ' map normal random number to uniform plane
    Dim nRows As Long: nRows = UBound(x, 1)
    Dim nCols As Long: nCols = UBound(x, 2)
    '
    Dim i As Long, j As Long
    For i = 1 To nRows
        For j = 1 To nCols
            x(i, j) = WorksheetFunction.NormSDist(x(i, j))
        Next j
    Next i
End Function
'
'
'
' VBA class module (name = IRandom)
Option Explicit
'
Public Function getNormalRandomMatrix( _
    ByVal nRows As Long, _
    ByVal nCols As Long) As Double()
    '
    ' interface - no implementation
    ' takes in two parameters (number of rows and columns) and
    ' returns double() filled with normal random variates
End Function
'
'
'
' VBA class module (name = MersenneTwister)
Option Explicit
'
Implements IRandom
'
Private Declare Function nextMT Lib "C:\temp\mt19937.dll" Alias "genrand" () As Double
'
Private Function IRandom_getNormalRandomMatrix( _
    ByVal nRows As Long, _
    ByVal nCols As Long) As Double()
    '
    ' retrieve NxM matrix with normal random numbers
    Dim r() As Double: ReDim r(1 To nRows, 1 To nCols)
    Dim i As Long, j As Long
    For i = 1 To nRows
        For j = 1 To nCols
            r(i, j) = InverseCumulativeNormal(nextMT())
        Next j
    Next i
    '
    IRandom_getNormalRandomMatrix = r
End Function
'
Public Function InverseCumulativeNormal(ByVal p As Double) As Double
    '
    ' Define coefficients in rational approximations
    Const a1 = -39.6968302866538
    Const a2 = 220.946098424521
    Const a3 = -275.928510446969
    Const a4 = 138.357751867269
    Const a5 = -30.6647980661472
    Const a6 = 2.50662827745924
    '
    Const b1 = -54.4760987982241
    Const b2 = 161.585836858041
    Const b3 = -155.698979859887
    Const b4 = 66.8013118877197
    Const b5 = -13.2806815528857
    '
    Const c1 = -7.78489400243029E-03
    Const c2 = -0.322396458041136
    Const c3 = -2.40075827716184
    Const c4 = -2.54973253934373
    Const c5 = 4.37466414146497
    Const c6 = 2.93816398269878
    '
    Const d1 = 7.78469570904146E-03
    Const d2 = 0.32246712907004
    Const d3 = 2.445134137143
    Const d4 = 3.75440866190742
    '
    'Define break-points
    Const p_low = 0.02425
    Const p_high = 1 - p_low
    '
    'Define work variables
    Dim q As Double, r As Double
    '
    'If argument out of bounds, raise error
    If p <= 0 Or p >= 1 Then Err.Raise 5
    '
    If p < p_low Then
        '
        'Rational approximation for lower region
        q = Sqr(-2 * Log(p))
        InverseCumulativeNormal = (((((c1 * q + c2) * q + c3) * q + c4) * q + c5) * q + c6) / _
        ((((d1 * q + d2) * q + d3) * q + d4) * q + 1)
        '
    ElseIf p <= p_high Then
        'Rational approximation for lower region
        q = p - 0.5
        r = q * q
        InverseCumulativeNormal = (((((a1 * r + a2) * r + a3) * r + a4) * r + a5) * r + a6) * q / _
        (((((b1 * r + b2) * r + b3) * r + b4) * r + b5) * r + 1)
        '
    ElseIf p < 1 Then
        'Rational approximation for upper region
        q = Sqr(-2 * Log(1 - p))
        InverseCumulativeNormal = -(((((c1 * q + c2) * q + c3) * q + c4) * q + c5) * q + c6) / _
        ((((d1 * q + d2) * q + d3) * q + d4) * q + 1)
    End If
End Function
'

Afterthoughts

In this version, Matrix class was replaced with plain two-dimensional array. Separate standard VBA module has been set to perform matrix operations (multiplication, transpose, cholesky decomposition, data input/output). Everything else is unchanged. With this small modification, we have reached reduction in processing times, when simulating correlated random numbers with Gaussian Copula model.

-Mike

Data structure for matrix in VBA

Large part of programming financial models has something to do with handling and operating matrices. However, for handling any matrix data, there is not ready-made data structure available for this purpose in VBA. The only way to get around this limitation, is to write your own custom data structure by using existing data structures, such as arrays. Within my previous posting on Gaussian Copula implementation, I created one such custom data structure, a Matrix class. Technically speaking, this class is just wrapping arrays into a manageable object with setters and getters, plus provides some of the most common matrix operations for the user.

The idea was very noble and I was quite happy with the first development candidate. I especially liked the idea of data structure being an object, also for schematic and semantic reasons. Plus, I thought that I would finally get rid of all those boring extra lines of code needed, when using plain arrays. I also thought that only a small performance penalty would be paid, with all function calls made using class accessors (push, at). However, as I was prototyping Monte Carlo basket equity option pricing and doing matrix operations with large matrices, I quickly realized that the cost of processing matrix operations was definitely way too high.

Testing processing times

The issue was bothering me in a such way, that I finally wanted to get some hard-tested facts on handling and operating matrix structures. For this reason, I prepared test cases for three different matrix schemes. Within these test cases, matrix data structure was implemented by using

1. Two-dimensional array
2. Variant array of double arrays (jagged array)
3. Matrix class

The use of Collection and Dictionary data structures has been left out of this experiment completely, since these data structures are empirically known to be more costly than the use of arrays. Nick Webber has been doing some serious woodshedding with these issues in his excellent book Implementing Models of Financial Derivatives: Object Oriented Applications with VBA within the chapter 16.

Within test cases mentioned, a simple procedural program performs the following operations for all matrix schemes described above

1. Creates three matrices (A, B, C)
2. Fills two matrices (A, B) with random numbers
3. Performs matrix multiplication (A, B) and returns the result into matrix (C)

Time elapsed was recorded only for the actual matrix multiplication operation. For each matrix schemes, matrix B rows (A columns) were dimensioned from 100 000  to 2 000 000 and matrix B columns (A rows) were assumed to be constant 10. For example, in the first calculation, we multiplied matrix A (10 * 100 000) with matrix B (100 000 * 10) and received matrix C (10 * 10). In the second calculation matrix dimensions were A (10 * 200 000) and B (200 000 * 10) and we received matrix C (10 * 10), and so on.

Cold shower

The following chart is presenting the findings of this experiment.



We can clearly see, that a simple two-dimensional array is the most efficient data structure for handling large matrix operations in VBA. There is just no way out of this, period. Testing program is presented below. You can just copy-paste it into a new standard VBA module, if you are interested to run it in your own laptop. Remember to create reference to Microsoft Scripting Runtime library.

Option Explicit
'
Private Declare Function GetTickCount Lib "kernel32.dll" () As Long
Private Const filePath As String = "C:\temp\matrix_log.txt"
Private fileSystem As Scripting.FileSystemObject
Private textWriter As TextStream
Private textWriterEnabled As Boolean
Private stream As String
Private startTime As Long
Private endTime As Long
Private timeElapsed As Double
'
Sub tester()
    '
    Set fileSystem = New Scripting.FileSystemObject
    Set textWriter = fileSystem.OpenTextFile(filePath, ForWriting, True)
    textWriterEnabled = True
    '
    Dim r As Long: r = 100000
    Dim c As Long: c = 10
    Dim i As Long
    For i = 0 To 19
        testRun_2DArray r + i * r, c
        testRun_arrayOfArrays r + i * r, c
        testRun_matrixClass r + i * r, c
    Next i
    '
    MsgBox "completed", vbInformation, "timer log file for matrix operations"
    Set textWriter = Nothing
    Set fileSystem = Nothing
End Sub
'
Private Function testRun_2DArray(ByVal r As Long, ByVal c As Long)
    '
    ' create 2-dim arrays needed
    Dim m1() As Double: ReDim m1(1 To r, 1 To c)
    Dim m2() As Double: ReDim m2(1 To c, 1 To r)
    Dim m3() As Double: ReDim m3(1 To c, 1 To c)
    Dim i As Long, j As Long, k As Long
    '
    ' fill array 1
    For i = 1 To r
        For j = 1 To c
            m1(i, j) = Rnd
        Next j
    Next i
    '
    ' fill array 2
    For i = 1 To r
        For j = 1 To c
            m2(j, i) = Rnd
        Next j
    Next i
    '
    ' perform matrix multiplication
    startTime = GetTickCount()
    Dim v As Double
    '
    For i = 1 To c
        For j = 1 To c
            v = 0
            '
            For k = 1 To r
                v = v + m2(i, k) * m1(k, j)
            Next k
            m3(i, j) = v
        Next j
    Next i
    '
    ' write timer results into log file
    endTime = GetTickCount()
    timeElapsed = (endTime - startTime) / 1000
    stream = "testRun_2DArray;" & r & ";" & timeElapsed
    If (textWriterEnabled) Then textWriter.WriteLine stream
End Function
'
Private Function testRun_arrayOfArrays(ByVal r As Long, ByVal c As Long)
    '
    ' create arrays of arrays needed
    Dim i As Long, j As Long, k As Long
    Dim inner() As Double
    '
    Dim m1() As Variant: ReDim m1(1 To r)
    For i = 1 To r
        ReDim inner(1 To c)
        m1(i) = inner
    Next i
    '
    Dim m2() As Variant: ReDim m2(1 To c)
    For i = 1 To c
        ReDim inner(1 To r)
        m2(i) = inner
    Next i
    '
    Dim m3() As Variant: ReDim m3(1 To c)
    For i = 1 To c
        ReDim inner(1 To c)
        m3(i) = inner
    Next i
    '
    ' fill array 1
    For i = 1 To r
        For j = 1 To c
            m1(i)(j) = Rnd
        Next j
    Next i
    '
    ' fill array 2
    For i = 1 To r
        For j = 1 To c
            m2(j)(i) = Rnd
        Next j
    Next i
    '
    ' perform matrix multiplication
    startTime = GetTickCount()
    Dim v As Double
    '
    For i = 1 To c
        For j = 1 To c
            v = 0
            '
            For k = 1 To r
                v = v + m2(i)(k) * m1(k)(j)
            Next k
            m3(i)(j) = v
        Next j
    Next i
    '
    ' write timer results into log file
    endTime = GetTickCount()
    timeElapsed = (endTime - startTime) / 1000
    stream = "testRun_arrayOfArrays;" & r & ";" & timeElapsed
    If (textWriterEnabled) Then textWriter.WriteLine stream
End Function
'
Private Function testRun_matrixClass(ByVal r As Long, ByVal c As Long)
    '
    ' create 2 matrix objects
    Dim m1 As New Matrix: m1.init r, c
    Dim m2 As New Matrix: m2.init c, r
    Dim i As Long, j As Long
    '
    ' fill matrix 1
    For i = 1 To r
        For j = 1 To c
            m1.push i, j, Rnd
        Next j
    Next i
    '
    ' fill matrix 2
    For i = 1 To c
        For j = 1 To r
            m2.push i, j, Rnd
        Next j
    Next i
    '
    ' perform matrix multiplication
    Dim m3 As New Matrix
    startTime = GetTickCount()
    Set m3 = m3.multiplication(m2, m1)
    '
    ' write timer results into log file
    endTime = GetTickCount()
    timeElapsed = (endTime - startTime) / 1000
    stream = "testRun_matrixClass;" & r & ";" & timeElapsed
    If (textWriterEnabled) Then textWriter.WriteLine stream
    '
    Set m3 = Nothing
    Set m2 = Nothing
    Set m1 = Nothing
End Function
'

Small matrices

Additionally, I also tested using MMULT function with simple two-dimensional arrays. Efficiency of this method is only marginally better, than using two-dimensional arrays with the code provided above (testRun_2DArray). Moreover, there is a limit of the sizes of matrices what we can feed for this worksheet function and those are surprisingly low. For example, trying to multiply A (10 * 100 000) with B (100 000 * 10) leads to runtime error.

The chart below is presenting the results for test cases with small matrices, including test case for using MMULT worksheet function. For each matrix schemes, matrix B rows (A columns) were dimensioned from 1 000  to 65 000 and matrix B columns (A rows) were assumed to be constant 10. For example, in the first calculation, we multiplied matrix A (10 * 1 000) with matrix B (1 000 * 10) and received matrix C (10 * 10). In the second calculation matrix dimensions were A (10 * 2 000) and B (2 000 * 10) and we received matrix C (10 * 10), and so on.



The direction of the results is the same as with large matrices. Using MMULT worksheet function is the most efficient choice, but only marginally better than using simple two-dimensional arrays. The use of Matrix wrapper class for small matrix operations can still be seen as reasonable choice, since the time loss compared to more efficient choices is after all, relatively small.

Final run

Just for the curious, I wanted to compare VBA matrix operations efficiency results with the corresponding C++ results. For this reason, I used dynamically allocated arrays. Otherwise, the actual testing program was basically the same as for VBA cases: allocate memory for arrays, fill arrays with random numbers, perform matrix multiplication and finally release the allocated memory. Time elapsed was recorded only for the actual matrix multiplication operation. The chart below is presenting the results.



In a nutshell, average efficiency ratio (VBA processing time / C++ processing time) is 5.24 for this experiment sample. Moreover, larger arrays can be handled in C++ than in VBA, since the memory is allocated from the heap memory instead of stack memory.

Afterthoughts

So, for any large and time-critical matrix operations performed in VBA, a simple two-dimensional array is the most efficient data structure which can be provided by VBA. For a small matrix operations, arrays wrapped in class can still be used. For real hardcore calculations (very large matrices, fast processing times), VBA is unfortunately not efficient tool for handling such calculations.

Life goes on - have a great weekend!

-Mike