QuantLib-Python: Multiprocessing Method Wrapper

In this post, I published a program for simulating term structure up to 30 years with daily time step, using Hull-White one-factor model. The resulting curve was able to replicate the given initial yield curve without any notable differences. The only serious issue here was the cost of running the program in time units.

In order to improve this specific issue, I got familiar with some multi-threading possibilities in Python. Now, there are some deep issues related to the way Python threads are actually implemented and especially the issues with thread locking known as GIL. Related stuff has been completely chewed in here. In order to avoid facing GIL-related issues, another way is to use Python multiprocessing, which allows the programmer to fully leverage multiple processors on a given machine. Moreover, separate processes are completely separate and one process cannot affect another's variables.

Comparison statistics

Again, I simulated term structure up to 30 years with daily time step, using 10000 paths. I did some quick profiling, in order to find the bottlenecks in the original program (sequential). By looking the column task share, we can see, that there are two tasks, which are consuming the most part of the complete running time: path generations (~54%) and path integrations (~46%). After this, I isolated these two parts and processed these by using multiprocessing scheme.

By using multiprocessing (two configured processes), I managed to decrease the complete running time from 163 seconds to 107 seconds. In general, for all those parts which were enjoying the benefits of multiprocessing, improvement ratio (multiprocessing per sequential) is around 0.65.

CPU puzzle

In order to understand the reason for this improvement, let us take a look at processor architecture in my laptop. First, let us check the "Grand Promise" made by System Monitor.

Based on this view, I actually expected to have four CPU for processing. I was then really surprised, that adding third and fourth process was not decreasing running time any further, than having just two processes. After some usual Stackoverflow gymnastics, I finally got the definition to calculate the real number of CPU available in my laptop.

CPU available is "Core(s) per socket * Socket(s)", which is 2 * 1 in my laptop. So, all in all I have only two CPU available for processing, not four as was shown in that System Monitor. This means, that having more than two CPU available in a laptop, one should expect even better improvement ratio than reported in my statistics here.

Wrapper method

In order to avoid code duplication and to come up with something a bit more generic, I started to dream about the possibility to create a mechanism for applying multiprocessing for any given method, if so desired. Such solution is possible by using Python lambda methods.

# method for executing given lambdas in parallel
def MultiprocessingWrapper(targetFunctionList):
    processList = []
    aggregatedResults = []
    queue = mp.Manager().Queue()

    # execute lambda from a given list based on a given index
    # storing results into queue
    def Worker(index):
        result = targetFunctionList[index]()
        queue.put(result)
    
    # start processes, call worker method with index number
    for i in range(len(targetFunctionList)):
        process = mp.Process(target = Worker, args = (i,))
        processList.append(process)
        process.start()
    
    # join processes, extract queue into results list
    for process in processList:
        process.join()
        aggregatedResults.append(queue.get())
        
    # return list of results for a client
    return aggregatedResults

Previous method is receiving a list of lambda methods as its argument. The idea is, that there would be always one lambda method for each process to be started. Why? We might face a situation, in which different set of parameters would be required for each lambda (say, all lambdas would be using the same uniform random generator, but with a different values for seeding the generator). In wrapper method, process is then created to start each configured lambda method. Results calculated by given lambda will be stored into queue. Finally, all results will be imported from queue into result list and returned for a client.

As concrete example, the following program segment is first creating two lambda methods for starting GeneratePaths method, but with different seed value for both processes. After this, wrapper method is then fed with the list of lambdas and processed paths will be received into list of results.

    # task of generating paths is highly time critical
    # use multiprocessing for path generation
    # create lambdas for multiprocessing wrapper
    # target signature: def GeneratePaths(seed, process, timeGrid, n)
    nPaths = 10000
    nProcesses = 2
    seeds = [1834, 66023]
    nPathsPerProcess = int(nPaths / nProcesses)
    target_1 = lambda:GeneratePaths(seeds[0], HW1F, grid.GetTimeGrid(), nPathsPerProcess)
    target_2 = lambda:GeneratePaths(seeds[1], HW1F, grid.GetTimeGrid(), nPathsPerProcess)
    targetFunctionList = [target_1, target_2]
    results = MultiprocessingWrapper(targetFunctionList)

The complete program can be found in my GitHub repository. Finally, a couple of discussion threads, which may be useful in order to understand some QuantLib-related issues, are given in here and here. Thanks for reading my blog and again, Merry Christmas for everyone.
-Mike
  

Excel : implementing multithreading using C# and Excel-DNA

Multithreading possibilities for VBA has been chewed in this post. My conclusion back then was, that there is no multi-threading possibilities for VBA. One reader has then been commenting this as follows :

"Correct to say there is no multithreading in VBA however, you can very easily create your multithreading functionality in a c# dll and expose the interface via Interops for VBA to consume. Then all you need to do is to pass in the data into the function and walla, you have multithreading. Interops is a very powerful feature and VBA fully supports it."

For the sake of completeness, I will present one possible program to implement such multithreading scheme for Excel, by using Parallel class for the actual multi-threading part and Excel-DNA for interfacing the program back to Excel (using Excel only as Input-Output platform). Excel interfacing part used in this post, has already been completely chewed within this post. Note, that by using instructions given in here or here, one can relatively easy interface this multithreading program back to VBA, instead of Excel.

The program

This unsurprising program is simply processing a task (simulate N amount of normally distributed random numbers) shared for M processors. Amount of simulated numbers and number of processors used is decided by the client (Excel). Finally, the program will print the aggregated time consumed for this task back to Excel. Needless to say, the effect of multithreading can be demonstrated by changing the number of processors in Excel worksheet.

Copy-Paste the following program presented below into a new C# project. Also, follow carefully all instructions given in this post.

Thanks for reading this blog.
-Mike

// ExcelInterface.cs
using System;
using System.Collections.Generic;
using System.Diagnostics;
using System.Threading.Tasks;
using System.Windows.Forms;
using ExcelDna.Integration;

namespace ExcelInterface {
    // type definition, delegate for exporting data from processor to queue
    using Processor = Action<int, DataMessenger>;
    public delegate void DataMessenger(List<double> result);

    public static class ExcelInterface {
        // method available in excel
        public static void execute() {
            try {
                // create Excel application object
                dynamic Excel = ExcelDnaUtil.Application;
                //
                // get parameters from worksheet named ranges
                int n = (int)Excel.Range["_n"].Value2;
                int nProcessors = (int)Excel.Range["_nProcessors"].Value2;
                int nPerProcessor = n / nProcessors;
                // create data thread-safe queue and random processors
                RandomQueue messageQueue = new RandomQueue();
                List<Processor> processors = new List<Processor>();
                for (int i = 0; i < nProcessors; ++i) {
                    processors.Add(Factory.CreateProcessor());
                }
                // host timer, execute all processors in parallel
                Stopwatch timer = new Stopwatch();
                timer.Start();
                Parallel.For(0, nProcessors, i => {
                    processors[i].Invoke(nPerProcessor, messageQueue.Enqueue); 
                });
                timer.Stop();
                //
                // print processing time to excel
                double timeElapsed = timer.Elapsed.TotalSeconds;
                Excel.Range["_timer"] = timeElapsed;
            }
            catch (Exception e) {
                MessageBox.Show(e.Message);
            }
        }
    }
}

// RandomQueue.cs
using System;
using System.Collections.Concurrent;
using System.Collections.Generic;

namespace ExcelInterface {
    // wrapper class for ConcurrentQueue data structure
    public class RandomQueue {
        private ConcurrentQueue<List<double>> randomQueue;
        public RandomQueue() {
            randomQueue = new ConcurrentQueue<List<double>>();
        }
        // add
        public void Enqueue(List<double> data) {
            randomQueue.Enqueue(data);
        }
        // remove
        public List<double> Dequeue() {
            List<double> data = null;
            bool hasValue = false;
            while (!hasValue) hasValue = randomQueue.TryDequeue(out data);
            return data;
        }
    }
}

// Factory.cs
using System;
using System.Collections.Generic;

namespace ExcelInterface {
    // type definition
    using Processor = Action<int, DataMessenger>;
    
    public static class Factory {
        // factory method for creating processor for random generator
        public static Processor CreateProcessor() {
            //
            // create standard normal variable generator
            // using action delegate and lambda expression
            Processor process =
            (int n, DataMessenger dataMessenger) => {
                Random generator = new Random(Guid.NewGuid().GetHashCode());
                List<double> normalRandomList = new List<double>();
                // loop through n
                for (int i = 0; i < n; ++i) {
                    double uniformRandomSum = 0.0;
                    // create standard normal random variable using CLT
                    for (int j = 0; j < 12; ++j) {
                        double uniformRandom = 0.0;
                        while (true) {
                            uniformRandom = generator.NextDouble();
                            if (uniformRandom > 0.0) break;
                        }
                        uniformRandomSum += uniformRandom;
                    }
                    normalRandomList.Add(uniformRandomSum - 6.0);
                }
                // send list of normal random variables to queue
                dataMessenger(normalRandomList);
            };
            return process;
        }
    }
}

C++11 : String Replacer for Directory Files using PPL

Sequential algorithms can be easily replaced with the corresponding Parallel Algorithms. However, these algorithms can only be applied, if the loop operations are completely independent and they are not using any shared variables. The second condition can be relaxed by using concurrent data structures. This scheme is perfect for cases, in which we need to process a chain of independent items, such as modifying files in a directory.

The devil is in the details

Let us think a real-life case, in which we have a lot of CSV files in one specific directory. For example, we may have transaction files (containing cash flow tables, date schedule tables, parameters) produced by some front office system batch on a daily basis. These files are then used as feed for a third-party analytical software for some intensive calculations. The only problem is, that some of the information in feed files is not in recognizable form for third-party software. In a nutshell, feed files may contain some specific strings, which should be replaced with another string.

War stories

The next question is how to do this operation quickly and on a safe manner? Needless to say, there are pretty much as many approaches as there are people performing this heartbreaking operation. Personally, I have used

• find-and-replace strategy with notepad++, until the amount of files to be processed and parameters to be replaced grew a bit too large.
• custom batch script, until I realized that the script was sometimes not working as expected, by either leaving some cases out from replacement operations or resulting incorrect replacements. The scariest part was, that the script was actually working well most of the time.
• custom Powershell script (created by someone else), which was using hard-coded configurations for all replacement strings and all strings which should be replaced. All configurations (hosted in source code file) needed to be set in a specific order. This was actually working well up to a point, where those hard-coded configurations should have been changed to correspond changes made in other systems. Moreover, execution times were a bit too high.

Finally, I decided to create my own program for handling this task.

United we fall, divided we stand

After learning a bit of parallel algorithms, I soon realized that this kind of a scheme (due to task independency) would be suitable candidate for implementing parallelism, in order to improve program execution speed. Each source file (containing transaction information) has to be processed separately and all key-value pairs (string-to-be-replaced and corresponding replacement string) can be stored in concurrent-safe concurrent unordered map as string pairs.

FileHandler.h

This header file is consisting free functions for all required file handling operations.

#pragma once
//
#include <filesystem>
#include <fstream>
#include <string>
#include <map>
#include <vector>
#include <algorithm>
#include <sstream>
//
namespace MikeJuniperhillFileSystemUtility
{
 std::string ReadFileContentToString(const std::string &filePathName)
 {
  std::string data;
  std::ifstream in(filePathName.c_str());
  std::getline(in, data, std::string::traits_type::to_char_type(
   std::string::traits_type::eof()));
  return data;
 }
 //
 void WriteStringContentToFile(const std::string& content, const std::string &filePathName)
 {
  std::ofstream out(filePathName.c_str());
  out << content;
  out.close();
 }
 //
 std::vector<std::string> GetDirectoryFiles(const std::string& folderPathName)
 {
  std::vector<std::string> directoryFiles;
  using itr = std::tr2::sys::directory_iterator;
  for (itr it = itr(folderPathName); it != itr(); ++it)
  {
   directoryFiles.push_back(static_cast<std::string>((*it).path()));
  }
  return directoryFiles;
 }
 //
 // replace all substrings found (stringToBeReplaced) with another 
 // string (replacementString) in a given string (string)
 std::string ReplaceAllSubstringsInString(const std::string& string, 
  const std::string& stringToBeReplaced, const std::string& replacementString)
 {
  std::string result;
  size_t find_len = stringToBeReplaced.size();
  size_t pos, from = 0;
  while (std::string::npos != (pos = string.find(stringToBeReplaced, from))) 
  {
   result.append(string, from, pos - from);
   result.append(replacementString);
   from = pos + find_len;
  }
  result.append(string, from, std::string::npos);
  return result;
 }
 // read key-value pairs into std::map
 // (key = string to be found and replaced, value = replacement string)
 std::map<std::string, std::string> ReadKeysFromFileToMap(const std::string& filePathName, char separator)
 {
  std::map<std::string, std::string> keys;
  std::ifstream file(filePathName);
  std::string stream;
  std::string key;
  std::string value;
  //
  while (std::getline(file, stream))
  {
   std::istringstream s(stream);
   std::getline(s, key, separator);
   std::getline(s, value, separator);
   keys.insert(std::pair<std::string, std::string>(key, value));
  }
  return keys;
 }
}
//

Tester.cpp

First, there has to be a directory containing all source files, which are going to be processed by file processing program. Also, there has to be a specific file, which contains key-value pairs (key = string to be found and replaced, value = replacement string) for all desired string replacement cases. Main program is creating file processors into vector container (there will be as many processors as there are source files to be processed). Then, main program is executing all file processors. A single file processor is first reading source file information into string, looping through all key-value pairs and checking whether any occurences are to be found, performing string replacements and finally, writing modified information back to original source file.

#include <ppl.h>
#include <concurrent_vector.h>
#include <concurrent_unordered_map.h>
#include <functional>
#include <memory>
#include <chrono>
#include <iostream>
#include "FileHandler.h"
//
namespace MJ = MikeJuniperhillFileSystemUtility;
//
using Files = std::vector<std::string>;
using Pair = std::pair<std::string, std::string>;
using Keys = std::map<std::string, std::string>;
using GlobalKeys = concurrency::concurrent_unordered_map<std::string, std::string>;
using ProcessorMethod = std::function<void(void)>;
using FileProcessor = std::shared_ptr<ProcessorMethod>;
//
// create file processor
FileProcessor Factory(const GlobalKeys& keys, const std::string& filePathName)
{
 // deferred execution
 ProcessorMethod processor = [=, &keys](void) -> void
 {
  std::string fileUnderProcessing = MJ::ReadFileContentToString(filePathName);
  for each (Pair pair in keys)
  {
   // extract key (string to be found and replaced) and value (replacement string)
   Pair keyValuePair = pair;
   std::string key = std::get<0>(keyValuePair);
   std::string value = std::get<1>(keyValuePair);
   //
   // check if key exists in a given string (containing all information in current file)
   size_t found = fileUnderProcessing.find(key);
   if (found != std::string::npos)
   {
    // if exists, replace key with value
    fileUnderProcessing = MJ::ReplaceAllSubstringsInString(fileUnderProcessing, key, value);
   }
  }
  // finally write change into original file
  MJ::WriteStringContentToFile(fileUnderProcessing, filePathName);
 };
 FileProcessor fileProcessor = FileProcessor(new ProcessorMethod(processor));
 return fileProcessor;
}
//
int main(int argc, char* argv[])
{
 // get required path strings from command line
 std::string keysFilePathName = argv[1];
 std::string fileDirectoryPathName = argv[2];
 //
 // create list of files (files to be modified) and list of key-value pairs 
 // (key = string to be found and replaced, value = replacement string)
 Files files = MJ::GetDirectoryFiles(fileDirectoryPathName);
 char separator = ',';
 Keys keys = MJ::ReadKeysFromFileToMap(keysFilePathName, separator);
 //
 // insert keys into concurrency-safe unordered map
 GlobalKeys Keys;
 std::for_each(keys.begin(), keys.end(),
  [&](Pair pair) -> void { Keys.insert(pair); });
 //
 // create file processors :
 // each processor will be processing exactly one file (given filePathName) 
 // by looping through all keys-value pairs (in GlobalKeys) and searching for 
 // all occurrences of substring (key) and replacing this with another string (value)
 std::vector<FileProcessor> processors;
 std::for_each(files.begin(), files.end(),
  [&](std::string filePathName) -> void { processors.push_back(Factory(Keys, filePathName)); });
 //
 // execute file processor method for all file processors
 auto start = std::chrono::steady_clock::now();
 concurrency::parallel_for_each(processors.begin(), processors.end(),
  [](FileProcessor fp) -> void { (*fp)(); });
 auto end = std::chrono::steady_clock::now();
 auto timeElapsed = std::chrono::duration_cast<std::chrono::seconds>(end - start);
 std::cout << "processed in " << timeElapsed.count() << " seconds" << std::endl;
 //
 return 0;
}
//

User settings

In this particular case, a picture is worth more than thousand words.

A : arguments for executable to be used with command prompt
B : directory for key-value pairs file
C : the content of key-value pairs file
D : directory for source files.

Finally, thanks a lot again for reading this blog.-Mike

C++11 : Multi-Threaded PathGenerator using PPL

 

FINAL DESTINATION

The circle has been closed. This post is kind of an aggregation, based on the last four posts published on generating random numbers. Initially, I started just with a simple template class for distributional random generator, then continued with a path generator using any one-factor stochastic process and finally, ended up with a multi-threaded distributional random generation scheme using Parallel algorithms. This final post (hopefully) is opening up my larger goal : to be able to generate asset price paths for any one-factor process, using multi-threading scheme.

GROUNDHOG DAY

Again, I have tested the both sequential (for_each) and parallel (parallel_for_each) schemes by using four generators, 10000 paths and 250 time steps for a single run. After this, I repeated this run for 250 times. Conclusion :

• The average running time for this sample was 17116 milliseconds (sequential) and 8209 milliseconds (parallel). So, parallel scheme will be completed about two times faster. 
• The actual CPU usage profiles during the simulation processes are behaving exactly as reported in this post. 
• I also analyzed processed asset price paths for parallel scheme, just to be absolutely sure there are no path duplicates (random number generation would not be independent). Based on my analysis made in Excel, all processed asset price paths are different and there are no duplicates. 

Presented scheme for path generator is again fulfilling my two initial requirements : faster creation of asset price paths following any one-factor process and independency of random generators.

RandomGenerator.h

The basic functionality of this template class has not been changed, except for construction part : second constructor is allowing a client to give any probability distribution for uniform generator from outside of this class. Even there is actually no need for having this kind of optionality in real-life (most of the stuff in Monte Carlo is randomized by using standard normal distribution), I decided to implement this optionality for the sake of completeness.

#pragma once
#include <algorithm>
#include <functional>
#include <vector>
#include <random>
#include <memory>
//
namespace MikeJuniperhillRandomGeneratorTemplate
{
 template <typename Generator = std::mt19937, typename Distribution = std::normal_distribution<double>>
 /// <summary>
 /// Template class for creating random number paths using mt19937 as default uniform 
 /// random generator and Standard Normal as default probability distribution.
 /// </summary> 
 class RandomGenerator
 {
 public:
  /// <summary>
  /// Constructor with explicit seed value
  /// </summary>
  RandomGenerator(unsigned long seed)
  {
   // construct function for processing distributional random number
   randomGenerator = [this](double x)-> double
   {
    x = distribution(uniformGenerator);
    return x;
   };
   // seed generator once
   uniformGenerator.seed(seed);
  }
  /// <summary> 
  /// Constructor for explicit seed value and client-given probability distribution.
  /// </summary>  
  RandomGenerator(unsigned long seed, const Distribution& distribution)
   // constructor delegation
   : RandomGenerator(seed)
  {
   // assign client-given probability distribution
   this->distribution = distribution;
  }
  /// <summary>
  /// Fill a given vector reference with distributional random numbers
  /// </summary> 
  void operator()(std::vector<double>& v) const
  {
   std::transform(v.begin(), v.end(), v.begin(), randomGenerator);
  }
 private:
  std::function<double(double)> randomGenerator;
  Generator uniformGenerator;
  Distribution distribution;
 };
}
//

OneFactorProcess.h

I decided to tag drift and diffusion functions with const declaration, since these functions should not modify the internal state of class data members.

#pragma once
//
namespace MikeJuniperhillOneFactorProcessLibrary
{
 /// <summary>
 /// Abstract base class for all one-factor processes for customizing 
 /// drift and diffusion functions for different types of processes.
 /// </summary>
 class OneFactorProcess
 {
 public:
  virtual double drift(double x, double t) const = 0;
  virtual double diffusion(double x, double t) const = 0;
 };
 //
 /// <summary>
 /// Implementation for Vasicek short-rate model.
 /// </summary>
 class Vasicek : public OneFactorProcess
 {
 public:
  Vasicek(double meanReversion, double longTermRate, double rateVolatility)
   : meanReversion(meanReversion), longTermRate(longTermRate), rateVolatility(rateVolatility) { }
  //
  double drift(double x, double t) const override { return meanReversion * (longTermRate - x); }
  double diffusion(double x, double t) const override { return rateVolatility; }
 private:
  double meanReversion;
  double longTermRate;
  double rateVolatility;
 };
}
//

PathGenerator.h

As in the case with RandomGenerator, the basic functionality of this template class has not been changed either, except for construction part : second constructor is allowing a client to give any probability distribution to be delivered for distributional random generator.

#pragma once
//
#include "RandomGenerator.h"
#include "OneFactorProcess.h"
namespace MJRandom = MikeJuniperhillRandomGeneratorTemplate;
namespace MJProcess = MikeJuniperhillOneFactorProcessLibrary;
//
namespace MikeJuniperhillPathGenerator
{
 template <typename Generator = std::mt19937, typename Distribution = std::normal_distribution<double>>
 class PathGenerator
 {
 public:
  /// <summary>
  /// Constructor for PathGenerator template class.
  /// </summary>
  PathGenerator(double spot, double maturity, unsigned long seed,
   const std::shared_ptr<MJProcess::OneFactorProcess>& process)
   : spot(spot), maturity(maturity), process(process)
  {
   // create random generator
   generator = std::unique_ptr<MJRandom::RandomGenerator<Generator, Distribution>>
    (new MJRandom::RandomGenerator<Generator, Distribution>(seed));
  }
  /// <summary>
  /// Constructor for PathGenerator template class, with a client-given probability distribution
  /// </summary>
  PathGenerator(double spot, double maturity, unsigned long seed,
   const std::shared_ptr<MJProcess::OneFactorProcess>& process, const Distribution& distribution)
   : spot(spot), maturity(maturity), process(process)
  {
   // create random generator with client-given probability distribution
   generator = std::unique_ptr<MJRandom::RandomGenerator<Generator, Distribution>>
    (new MJRandom::RandomGenerator<Generator, Distribution>(seed, distribution));
  }
  /// <summary> 
  /// Fill a given vector reference with asset prices, following a given stochastic process.
  /// </summary>  
  void operator()(std::vector<double>& v) const
  {
   // transform initialized vector into a path containing random numbers
   (*generator)(v);
   //
   double dt = maturity / (v.size() - 1);
   double dw = 0.0;
   double s = spot;
   double t = 0.0;
   v[0] = s; // 1st path element will always be the current spot price
   //
   // transform distributional random number vector into a path containing 
   // asset prices from a given stochastic one-factor process
   for (auto it = v.begin() + 1; it != v.end(); ++it)
   {
    t += dt;
    dw = (*it) * std::sqrt(dt);
    (*it) = s + (*process).drift(s, t) * dt + (*process).diffusion(s, t) * dw;
    s = (*it);
   }
  }
 private:
  double spot;
  double maturity;
  std::shared_ptr<MJProcess::OneFactorProcess> process;
  std::unique_ptr<MJRandom::RandomGenerator<Generator, Distribution>> generator;
 };
}
//

Tester.cpp

Tester program is closely tracking the program presented in previous post. For the sake of additional clarity, I have used new type definitions in order to improve code readability and get rid of some lengthy variable names. The program is again using simple factory method for creating PathGenerator (function wrapped in shared pointer). In this program, OneFactorProcess implementation is created and delivered for factory method for processing. Finally, there is a method for printing processed paths to console for testing purposes.

#include <iostream>
#include <chrono>
#include <ppl.h>
#include <concurrent_vector.h>
#include "PathGenerator.h"
namespace MJGenerator = MikeJuniperhillPathGenerator;
//
// type definitions
using Path = std::vector<double>;
using Paths = concurrency::concurrent_vector<Path>;
using Process = std::shared_ptr<MJProcess::OneFactorProcess>;
using Processor = std::function<void(void)>;
using PathGenerator = std::shared_ptr<Processor>;
//
// thread-safe container for storing asset price paths, processed by path generators
Paths paths;
//
// printer for generated asset price paths
void Printer()
{
 std::for_each(paths.begin(), paths.end(),
  [](Path path) -> void
 {
  std::for_each(path.begin(), path.end(),
   [](double s) -> void
  {
   std::cout << s << ",";
  });
  std::cout << std::endl;
 });
}
//
// factory method :
// return path-generating function as function wrapper
// input arguments are common for all types of generators
PathGenerator Factory(double spot, double maturity, int nPaths, 
 int nSteps, unsigned long seed, const Process& process, Paths& paths)
{
 // create function for processing one-factor paths
 auto generator = [=, &process, &paths]() -> void
 {
  MJGenerator::PathGenerator<> oneFactorProcess(spot, maturity, seed, process);
  Path path(nSteps);
  for (auto i = 0; i != nPaths; ++i)
  {
   oneFactorProcess(path);
   paths.push_back(path);
  }
 };
 // return generator function as function wrapper
 return PathGenerator(new Processor(generator));
}
//
int main()
{
 // create vasicek process
 double longTermRate = 0.05;
 double meanReversion = 0.2;
 double rateVolatility = 0.0075; 
 Process vasicek = Process(new MJProcess::Vasicek(meanReversion, longTermRate, rateVolatility));
 //
 // define parameters and seed values for path generators
 int nGenerators = 4;
 int nPaths = 100;
 int nSteps = (250 + 1);
 std::vector<unsigned long> seed = { 10322854, 65947, 387528, 772399573 };
 //
 // use factory method for creating path generators
 double spot = 0.0095;
 double maturity = 3.0;
 std::vector<PathGenerator> generators;
 for (auto i = 0; i < nGenerators; i++) generators.push_back(
  Factory(spot, maturity, nPaths, nSteps, seed[i], vasicek, paths));
 //
 // parallel processing
 auto start = std::chrono::steady_clock::now();
 concurrency::parallel_for_each(generators.begin(), generators.end(),
  [](PathGenerator pg) -> void { (*pg)(); });
 auto end = std::chrono::steady_clock::now();
 auto timeElapsed = std::chrono::duration_cast<std::chrono::milliseconds>(end - start);
 std::cout << timeElapsed.count() << std::endl;
 //
 // print paths
 Printer();
 return 0;
}
//

Finally, thanks again for reading this blog.
-Mike

C++11 : Multi-Threaded Random Generator using PPL

After some woodshedding with C++11 random and publishing distributional random generator in my blog a couple of weeks ago, the next question was, how to make this thing to happen a bit faster? Since I already have been snooping PPL (Parallel Patterns Library), I realized that Parallel Algorithms in that library would be an excellent candidate for this task. There is a great and comprehensive internet book available on this topic. After getting familiar with some of the issues presented in these sources, one should be able to parallelize algorithms succesfully.

There are some very specific issues, related to random generator seeding. As I started to parallelize my random number generation (creating several generators and processing these using parallel algorithm), I realized that my random generators were not working as expected. After some further woodshedding I came to conclusion, that (in a multi-threaded setting) each generator has to be seeded independently. Finally, concerning my current generator implementation, I made a decision that a client has to provide explicit seed values for all generators. Based on my hands-on experience with a system used for counterparty credit risk simulations (widely ranked as state-of-the-art numerical software), I dare to say that this approach is well justified. Now, the question of what kind of tools will be used for creating the actual seed values, has been left to a client judgement. The rabbit hole of these profound issues related to random generators have been chewed in this blog. Do not enter, if you are not absolutely ready to take the red pill.

ROUGH DIAGNOSTICS

I tested the both sequential (for_each) and parallel (parallel_for_each) schemes by using four generators, 10000 paths and 250 time steps for a single run. After this, I repeated this run for 250 times. The average running time for this sample was 5187 milliseconds (sequential) and 2317 milliseconds (parallel). So, parallel scheme will be completed about two times faster. The actual CPU usages during simulation process for the both schemes are shown in the screenshot below. When using parallel algorithm, computer is able to utilize all four cores in my computer.

I also tested all processed random paths for the both schemes, just to be absolutely sure there are no path duplicates (random number generation would not be independent). Based on my analysis made in Excel, all processed paths for the both schemes are different and there are no duplicates. Presented scheme is hereby fulfilling my two requirements : faster creation of random paths and independency of random generators.

RandomGenerator.h

Current implementation for distributional random path generator is presented below. Note, that the actual seeder creation takes place outside of this class.

#pragma once
#include <algorithm>
#include <functional>
#include <vector>
#include <random>
//
namespace MikeJuniperhillRandomGeneratorTemplate
{
 template <typename Generator = std::mt19937, typename Distribution = std::normal_distribution<double>>
 /// <summary>
 /// Template class for creating random number paths using
 /// Mersenne Twister as default uniform random generator and
 /// Standard Normal (0.0, 1.0) as default probability distribution.
 /// </summary> 
 class RandomGenerator
 {
 public:
  /// <summary>
  /// set explicit seed value
  /// </summary>
  RandomGenerator(unsigned long seed)
  {
   // construct lambda method for processing standard normal random number
   randomGenerator = [this](double x)-> double
   {
    x = distribution(uniformGenerator);
    return x;
   };
   // seed generator
   uniformGenerator.seed(seed);
  }
  /// <summary>
  /// fill vector reference with distributional random numbers
  /// </summary> 
  void operator()(std::vector<double>& v)
  {
   std::transform(v.begin(), v.end(), v.begin(), randomGenerator);
  }
 private:
  std::function<double(double)> randomGenerator;
  Generator uniformGenerator;
  Distribution distribution;
 };
}
//

tester.cpp

First, all simulation parameters and explicit seed values for all generators are defined. Simple factory method is then used to create the actual generator function as lambda function. Next, factory method is returning generator function wrapped inside a shared pointer. Main program is then storing each created generator function into vector container and finally processing all generators (sequentially or parallel). Each generator is storing generated paths into thread-safe nested vector (std::vector inside concurrency::concurrent_vector).

#include <iostream>
#include <memory>
#include <chrono>
#include <ppl.h>
#include <concurrent_vector.h>
#include "RandomGenerator.h"
namespace MJ = MikeJuniperhillRandomGeneratorTemplate;
//
//
// thread-safe nested vector for storing random paths processed by generators
concurrency::concurrent_vector<std::vector<double>> paths;
//
// prototype for generator function
using Generator = std::function<void(void)> ;
//
// factory method :
// return generator function as function wrapper
std::shared_ptr<Generator> Factory(int nPaths, int nSteps, unsigned long seed, 
 concurrency::concurrent_vector<std::vector<double>>& paths)
{
 // create generator function
 auto generator = [=, &paths]()->void
 {
  // step 1 : create distributional random generator
  MJ::RandomGenerator<> randomGenerator(seed);
  // step 2 : create container for a random path
  std::vector<double> path(nSteps);
  // step 3 : create path using distributional generator
  // and import created path into thread-safe container
  for (auto i = 0; i != nPaths; ++i)
  {
   randomGenerator(path);
   paths.push_back(path);
  }
 };
 // return generator function as function wrapper
 return std::shared_ptr<Generator>(new Generator(generator));
}
//
int main()
{
 // define parameters and seed values for generator functions
 int nGenerators = 4;
 int nPaths = 10000;
 int nSteps = 250;
 std::vector<unsigned long> seed = { 10322854, 65947, 387528, 772399573 };
 //
 // use factory method for creating generator function
 std::vector<std::shared_ptr<Generator>> generators;
 for (auto i = 0; i < nGenerators; i++) generators.push_back(Factory(nPaths, nSteps, seed[i], paths));
 //
 // parallel processing
 auto start = std::chrono::steady_clock::now();
 concurrency::parallel_for_each(generators.begin(), generators.end(),
  [](std::shared_ptr<Generator> ppg) -> void { (*ppg)(); });
 //
 //// uncomment for sequential processing
 //std::for_each(generators.begin(), generators.end(),
 // [](std::shared_ptr<Generator> ppg) -> void { (*ppg)(); });
 //
 auto end = std::chrono::steady_clock::now();
 auto timeElapsed = (end - start);
 std::cout << std::chrono::duration_cast<std::chrono::milliseconds>(timeElapsed).count() << std::endl;
 return 0;
}
//

Finally, thanks for reading my blog. I would like to wish Happy New Year for everybody.
-Mike

Multi-Threaded Copula producer in C#

I wanted to publish one more article for the sake of celebrating the end of the year 2014. This time I am opening one possible solution for producing multi-threaded correlated random numbers with Gaussian Copula in C#. The numerical scheme used for this procedure has already been opened well enough in this blog posting. Usually, programs presented in this blog have been having (more or less) something to do with Microsoft Excel. This time, there is only C# program. However, with all the example programs presented in this blog, the user should be able to interface this program back to Excel in many different ways, if so desired.

PRODUCER-CONSUMER

In this simple example program, Producer-Consumer Pattern has been used. CopulaQueue class is nothing more, than just a wrapper for thread-safe ConcurrentQueue data structure. More specifically, the part of the program which actually creates all correlated random numbers into CopulaQueue, is the Producer. In the program, concrete CopulaEngine implementation class takes concrete RandomGenerator implementation class and correlation matrix as its input parameters. Concrete CopulaEngine implementation class then creates correlated random numbers and uses C# Event for sending created random number matrices to CopulaQueue. Another part of the program is the Consumer. Here, I have created a simple consumer class which simply prints created random numbers to console. Consumer class also uses C# Event for Dequeueing random number matrices from CopulaQueue. Needless to say, this (Consumer) is the part of our program, where we should be utilizing all correlated random numbers created by the Producer.

On design side, this program is closely following the program presented in the blog posting referred above. Again, the beef in this design is on its flexibility to allow any new implementations for Random generator and Copula model. Moreover, our example program is using C# Framework Parallel class method Parallel.ForEach, found under System.Threading.Tasks namespace. Example program creates four producers and consumers (both into List data structure) and using multi-threading (Parallel.ForEach) when processing correlated random numbers into/from CopulaQueue.

C# PROGRAM

In order to make everything as smooth as possible for the program replication, I have been writing all required classes in the same file. Just create a new console application and copy-paste the following program into a new .cs file.

using System;
using System.Diagnostics;
using System.Linq;
using System.Collections.Generic;
using System.Threading.Tasks;
using System.Collections.Concurrent;
//
namespace MultithreadingCopula
{
    // public delegate methods needed for sending and receiving matrix data
    public delegate void MatrixSender(double[,] matrix);
    public delegate double[,] MatrixReceiver();
    // ********************************************************************
    //
    // the main program 
    class Program
    {
        static void Main(string[] args)
        {
            try
            {
                // start timer
                Stopwatch timer = new Stopwatch();
                timer.Start();
                //
                // PRODUCER PART
                // create copula implementation, correlation matrix data and list of copula engines
                CopulaQueue copulaQueue = new CopulaQueue();
                double[,] correlationMatrix = createCorrelationMatrix();
                List<CopulaEngine> engines = new List<CopulaEngine>();
                int nEngines = 4;
                int nRandomArrays = 25000;
                for (int i = 0; i < nEngines; i++)
                {
                    engines.Add(new GaussianCopula(nRandomArrays, correlationMatrix, new CSharpRandom()));
                    ((GaussianCopula)engines[i]).SendMatrix += copulaQueue.Enqueue;
                }
                // process all copula engines (producers) in parallel
                Parallel.ForEach(engines, engine => engine.Process());
                //
                // CONSUMER PART
                // create list of consumers
                List<Consumer> consumers = new List<Consumer>();
                int nConsumers = nEngines;
                for (int i = 0; i < nConsumers; i++)
                {
                    consumers.Add(new Consumer(nRandomArrays, "consumer_" + (i + 1).ToString()));
                    consumers[i].ReceiveMatrix += copulaQueue.Dequeue;
                }
                // process all consumers in parallel
                Parallel.ForEach(consumers, consumer => consumer.Process());
                //
                // stop timer, print elapsed time to console
                timer.Stop();
                Console.WriteLine("{0}  {1}", "time elapsed", timer.Elapsed.TotalSeconds.ToString());
            }
            catch (AggregateException e)
            {
                Console.WriteLine(e.Message.ToString());
            }
        }
        // hard-coded data for correlation matrix
        static double[,] createCorrelationMatrix()
        {
            double[,] correlation = new double[5, 5];
            correlation[0, 0] = 1.0; correlation[0, 1] = 0.748534249620189;
            correlation[0, 2] = 0.751; correlation[0, 3] = 0.819807151586399;
            correlation[0, 4] = 0.296516443152486; correlation[1, 0] = 0.748534249620189;
            correlation[1, 1] = 1.0; correlation[1, 2] = 0.630062355599386;
            correlation[1, 3] = 0.715491543000545; correlation[1, 4] = 0.329358787086333;
            correlation[2, 0] = 0.751; correlation[2, 1] = 0.630062355599386;
            correlation[2, 2] = 1.0; correlation[2, 3] = 0.758158276137995;
            correlation[2, 4] = 0.302715778081627; correlation[3, 0] = 0.819807151586399;
            correlation[3, 1] = 0.715491543000545; correlation[3, 2] = 0.758158276137995;
            correlation[3, 3] = 1.0; correlation[3, 4] = 0.286336231914179;
            correlation[4, 0] = 0.296516443152486; correlation[4, 1] = 0.329358787086333;
            correlation[4, 2] = 0.302715778081627; correlation[4, 3] = 0.286336231914179;
            correlation[4, 4] = 1.0;
            return correlation;
        }
    }
    // ********************************************************************
    //
    // consumer class for correlated random numbers
    public class Consumer
    {
        public event MatrixReceiver ReceiveMatrix;
        public string ID;
        private int n;
        //
        public Consumer(int n, string ID) { this.n = n; this.ID = ID; }
        public void Process()
        {
            for (int i = 0; i < n; i++)
            {
                // get correlated 1xM random matrix from CopulaQueue and print it to console
                double[,] matrix = ReceiveMatrix();
                Console.WriteLine("{0}  {1}  {2}  {3}  {4}  {5}", this.ID, Math.Round(matrix[0, 0], 4), 
                    Math.Round(matrix[0, 1], 4), Math.Round(matrix[0, 2], 4), 
                    Math.Round(matrix[0, 3], 4), Math.Round(matrix[0, 4], 4));
                //
            }
        }
    }
    // ********************************************************************
    //
    // abstract base class for all uniform random generators
    public abstract class RandomGenerator
    {
        public abstract double GetUniformRandom();
    }
    // ********************************************************************
    //
    // uniform random generator implementation by using CSharp Random class
    public class CSharpRandom : RandomGenerator
    {
        private Random generator;
        //
        public CSharpRandom()
        {
            // using unique GUID hashcode as a seed
            generator = new Random(Guid.NewGuid().GetHashCode());
        }
        public override double GetUniformRandom()
        {
            // Random.NextDouble method returns a double greater than or equal to 0.0 
            // and less than 1.0. Built-in checking procedure prevents out-of-bounds random 
            // number to be re-distributed further to CopulaEngine implementation.
            double rand = 0.0;
            while (true)
            {
                rand = generator.NextDouble();
                if (rand > 0.0) break;
            }
            return rand;
        }
    }
    // ********************************************************************
    //
    // abstract base class for all specific copula implementations
    public abstract class CopulaEngine
    {
        // Uniform random generator and correlation matrix are hosted in this abstract base class.
        // Concrete classes are providing algorithm implementation for a specific copula
        // and event mechanism for sending created correlated random numbers matrix data to CopulaQueue class.
        protected RandomGenerator generator;
        protected double[,] correlation;
        //
        public CopulaEngine(double[,] correlation, RandomGenerator generator)
        {
            this.correlation = correlation;
            this.generator = generator;
        }
        public abstract void Process();
    }
    // ********************************************************************
    //
    // concrete implementation for gaussian copula
    public class GaussianCopula : CopulaEngine
    {
        public event MatrixSender SendMatrix;
        private double[,] normalRandomMatrix;
        private double[,] choleskyMatrix;
        private double[,] correlatedNormalRandomMatrix;
        private double[,] correlatedUniformRandomMatrix;
        private int rows;
        private int cols;
        //
        public GaussianCopula(int n, double[,] correlation, RandomGenerator generator)
            : base(correlation, generator)
        {
            this.cols = base.correlation.GetUpperBound(0) + 1; // M, number of variables
            this.rows = n; // N, number of 1xM matrices
        }
        public override void Process()
        {
            // NxM matrix containing of uniformly distributed correlated random variables are calculated 
            // as a sequence of specific matrix operations
            createNormalRandomMatrix();
            createCholeskyMatrix();
            correlatedNormalRandomMatrix = MatrixTools.Transpose(MatrixTools.Multiplication(choleskyMatrix, MatrixTools.Transpose(normalRandomMatrix)));
            createCorrelatedUniformRandomMatrix();
        }
        private void createNormalRandomMatrix()
        {
            // create NxM matrix consisting of normally distributed independent random variables
            normalRandomMatrix = new double[rows, cols];
            for (int i = 0; i < rows; i++)
            {
                for (int j = 0; j < cols; j++)
                {
                    normalRandomMatrix[i, j] = StatTools.NormSInv(base.generator.GetUniformRandom());
                }
            }
        }
        private void createCholeskyMatrix()
        {
            // create lower-triangular NxM cholesky decomposition matrix
            choleskyMatrix = new double[cols, cols];
            double s = 0.0;
            //
            for (int j = 1; j <= cols; j++)
            {
                s = 0.0;
                for (int k = 1; k <= (j - 1); k++)
                {
                    s += Math.Pow(choleskyMatrix[j - 1, k - 1], 2.0);
                }
                choleskyMatrix[j - 1, j - 1] = base.correlation[j - 1, j - 1] - s;
                if (choleskyMatrix[j - 1, j - 1] <= 0.0) break;
                choleskyMatrix[j - 1, j - 1] = Math.Sqrt(choleskyMatrix[j - 1, j - 1]);
                //
                for (int i = j + 1; i <= cols; i++)
                {
                    s = 0.0;
                    for (int k = 1; k <= (j - 1); k++)
                    {
                        s += (choleskyMatrix[i - 1, k - 1] * choleskyMatrix[j - 1, k - 1]);
                    }
                    choleskyMatrix[i - 1, j - 1] = (base.correlation[i - 1, j - 1] - s) / choleskyMatrix[j - 1, j - 1];
                }
            }
        }
        private void createCorrelatedUniformRandomMatrix()
        {
            // map normally distributed numbers back to uniform plane
            // process NxM matrix row by row
            for (int i = 0; i < rows; i++)
            {
                // create a new 1xM matrix for each row and perform uniform transformation
                correlatedUniformRandomMatrix = new double[1, cols];
                for (int j = 0; j < cols; j++)
                {
                    correlatedUniformRandomMatrix[0, j] = StatTools.NormSDist(correlatedNormalRandomMatrix[i, j]);
                }
                // event : send transformed 1xM matrix to CopulaQueue
                this.SendMatrix(correlatedUniformRandomMatrix);
            }
        }
    }
    // ********************************************************************
    //
    // this is technically just a wrapper class for ConcurrentQueue data structure
    public class CopulaQueue
    {
        private ConcurrentQueue<double[,]> queue;
        public CopulaQueue()
        {
            queue = new ConcurrentQueue<double[,]>();
        }
        public void Enqueue(double[,] matrix)
        {
            // insert a matrix into data structure
            queue.Enqueue(matrix);
        }
        public double[,] Dequeue()
        {
            // remove a matrix from data structure
            double[,] matrix = null;
            bool hasValue = false;
            while (!hasValue) hasValue = queue.TryDequeue(out matrix);
            return matrix;
        }
    }
    // ********************************************************************
    //
    // collection of methods for different types of statistical calculations
    public static class StatTools
    {
        // rational approximation for the inverse of standard normal cumulative distribution. 
        // the distribution has a mean of zero and a standard deviation of one.
        // source : Peter Acklam web page home.online.no/~pjacklam/notes/invnorm/
        public static double NormSInv(double x)
        {
            const double a1 = -39.6968302866538; const double a2 = 220.946098424521;
            const double a3 = -275.928510446969; const double a4 = 138.357751867269;
            const double a5 = -30.6647980661472; const double a6 = 2.50662827745924;
            //
            const double b1 = -54.4760987982241; const double b2 = 161.585836858041;
            const double b3 = -155.698979859887; const double b4 = 66.8013118877197;
            const double b5 = -13.2806815528857;
            //
            const double c1 = -7.78489400243029E-03; const double c2 = -0.322396458041136;
            const double c3 = -2.40075827716184; const double c4 = -2.54973253934373;
            const double c5 = 4.37466414146497; const double c6 = 2.93816398269878;
            //
            const double d1 = 7.78469570904146E-03; const double d2 = 0.32246712907004;
            const double d3 = 2.445134137143; const double d4 = 3.75440866190742;
            //
            const double p_low = 0.02425; const double p_high = 1.0 - p_low;
            double q = 0.0; double r = 0.0; double c = 0.0;
            //
            if ((x > 0.0) && (x < 1.0))
            {
                if (x < p_low)
                {
                    // rational approximation for lower region
                    q = Math.Sqrt(-2.0 * Math.Log(x));
                    c = (((((c1 * q + c2) * q + c3) * q + c4) * q + c5) * q + c6) / ((((d1 * q + d2) * q + d3) * q + d4) * q + 1);
                }
                if ((x >= p_low) && (x <= p_high))
                {
                    // rational approximation for middle region
                    q = x - 0.5; r = q * q;
                    c = (((((a1 * r + a2) * r + a3) * r + a4) * r + a5) * r + a6) * q / (((((b1 * r + b2) * r + b3) * r + b4) * r + b5) * r + 1);
                }
                if (x > p_high)
                {
                    // rational approximation for upper region
                    q = Math.Sqrt(-2 * Math.Log(1 - x));
                    c = -(((((c1 * q + c2) * q + c3) * q + c4) * q + c5) * q + c6) / ((((d1 * q + d2) * q + d3) * q + d4) * q + 1);
                }
            }
            else
            {
                // throw if given x value is out of bounds (less or equal to 0.0, greater or equal to 1.0) 
                throw new Exception("input parameter out of bounds");
            }
            return c;
        }
        public static double NormSDist(double x)
        {
            // returns the standard normal cumulative distribution function. 
            // the distribution has a mean of zero and a standard deviation of one.
            double sign = 1.0;
            if (x < 0) sign = -1.0;
            return 0.5 * (1.0 + sign * errorFunction(Math.Abs(x) / Math.Sqrt(2.0)));
        }
        private static double errorFunction(double x)
        {
            // uses Hohner's method for improved efficiency.
            const double a1 = 0.254829592; const double a2 = -0.284496736;
            const double a3 = 1.421413741; const double a4 = -1.453152027;
            const double a5 = 1.061405429; const double a6 = 0.3275911;
            x = Math.Abs(x); double t = 1 / (1 + a6 * x);
            return 1 - ((((((a5 * t + a4) * t) + a3) * t + a2) * t) + a1) * t * Math.Exp(-1 * x * x);
        }
    }
    // ********************************************************************
    //
    // collection of methods for different types of matrix operations
    public static class MatrixTools
    {
        public static double[,] Transpose(double[,] matrix)
        {
            // method for transposing matrix
            double[,] result = new double[matrix.GetUpperBound(1) + 1, matrix.GetUpperBound(0) + 1];
            //
            for (int i = 0; i < matrix.GetUpperBound(0) + 1; i++)
            {
                for (int j = 0; j < matrix.GetUpperBound(1) + 1; j++)
                {
                    result[j, i] = matrix[i, j];
                }
            }
            return result;
        }
        public static double[,] Multiplication(double[,] matrix1, double[,] matrix2)
        {
            // method for matrix multiplication
            double[,] result = new double[matrix1.GetUpperBound(0) + 1, matrix2.GetUpperBound(1) + 1];
            double v = 0.0;
            //
            for (int i = 0; i < matrix1.GetUpperBound(0) + 1; i++)
            {
                for (int j = 0; j < matrix2.GetUpperBound(1) + 1; j++)
                {
                    v = 0.0;
                    for (int k = 0; k < matrix1.GetUpperBound(1) + 1; k++)
                    {
                        v += matrix1[i, k] * matrix2[k, j];
                    }
                    result[i, j] = v;
                }
            }
            return result;
        }
    }
}

TEST RUN

When running the program, I get the following console printout. The printout shows, how our four consumers used in the example program are Dequeueing correlated 1x5 random matrices from CopulaQueue in parallel.

EFFICIENCY AND CORRELATION

One million rows for 5x5 correlation matrix was processed 100 times, when testing efficiency of the producer part of the program. More specifically, four producers (CopulaEngine) are creating 1x5 matrices, consisting of five correlated uniformly distributed random numbers one by one and then sending these matrices to ConcurrentQueue wrapped in CopulaQueue class in parallel. Each of the four producers are then performing this operation 250 thousand times. Finally, the whole operation was repeated 1 hundred times and time elapsed for each repetition was saved for further analysis. The results of this experiment are reported in the table below.

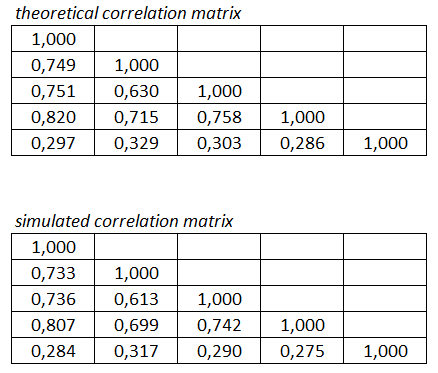
As we can see in the table, multi-threading is nicely reducing processing time, but in a non-linear fashion. Next, I printed out one batch of correlated random numbers (1000000x5 matrix) into text file and compared theoretical and simulated correlation in Excel. Results are reported in the table below. We can see, that simulated correlation is in line with theoretical correlation (enough, IMHO).

READING REFERENCES

For me personally, the following two books are standing in their own class. Ben and Joseph Albahari C# in a nutshell is presenting pretty much everything one has to know (and a lot more) about C# and especially on .NET framework. Very nice thing is also, that Albahari brothers have been kindly offering a free chapter on multi-threading from this book on their website. Daniel Duffy and Andrea Germani C# for financial markets is presenting how to apply C# in financial programs. There are a lot of extremely useful examples on multi-threaded programs, especially on using multi-threading in Monte Carlo applications and the general usage of Producer-Consumer pattern, when using multi-threading.

Again, Big thanks for reading my blog and Happy and Better New Year 2015 for everybody.

-Mike