MoCaX: Using Chebyshev Tensors for Computational Bottlenecks in Risk Calculations

Even this Machine Learning has been the hottest hype already for years, I have personally still had very vague understanding of how this thing could be applied in risk management domain. This post is presenting one such application: Chebyshev Tensors for getting rid of computational bottlenecks in risk calculations.

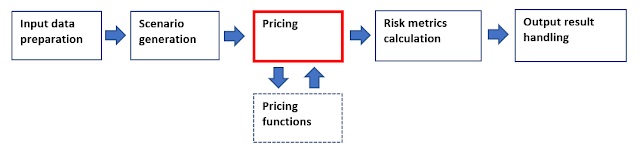
All risk management people are familiar with the following generic steps.

The sequence is describing steps for the most types of computationally-intensive risk calculations. In here, pricing (revaluation of financial transactions) is the step, which makes these calculations computationally intensive, since there will usually be substantial amount of revaluation calls sent to all kinds of pricing functions. For this reason, processing times will usually explode and this will costs us time.

In the past, the banks have usually tried to resolve these computational bottlenecks by acquiring more computational muscle and relying on multi-processing schemes. However, for a large enough player with an active derivatives book containing exotic products, even these attempts might not be enough to resolve the issue. Since the burden of producing all kinds of regulatory measures seems to be just growing, there is simply more calculations to be processed, than we have hours within one day.

Chebyshev Tensors

Another way to resolve such computational issues is to find clever algorithmic approximations and that's where Chebyshev Tensors are amazing. In a nutshell, by using Chebyshev Tensors we can create extremely accurate replicas of our standard pricing functions and use them instead of our original time-consuming function in calculations..

Interpolation methods through polynomials can deliver exponential convergence to the original function, when the interpolating points are Chebyshev points. Also, derivatives of the polynomial converge exponentially to the derivatives of the original function. Finally, Chebyshev Tensors can be extended to higher dimensions.

Example: 1-dimensional MoCaX approximation on valuing European call options

First, let us value a portfolio of European call options, where the spot price varies between 50 and 150. We divide this spot price range into one million steps. Other parameters in the model are constants. We get total of one million calculation tasks and one million revaluation calls to our pricing function. Note, that processing time is about 330 seconds (5.5 minutes) to complete all calculations. 

Next, we calculate the approximations for exactly the same set of option values, but we give only 25 analytically-valued option values for Mocax object and the rest of the values will be interpolated by Mocax object. Processing time is about 5.2 seconds to complete all calculation. Maximum error is around 1.5e-12, which is already quite close to machine precision. Error function (analytical values minus approximated values) is shown below. 

So, with just 25 Chebyshev points in our grid, we get remarkably close to the original pricing function values just with the fraction of original processing time. I dare to describe this as nothing less than impressive. This simple example just quickly scratches the surface, since one can imagine the application areas in risk management calculations are endless. Some of these application areas are well described in the book by Ignacio Ruiz and Mariano Zeron.

Let us go through the code. First, we need to import MoCaX library.

import mocaxpy

After this, we create MoCax object. In constructor, the first argument could be a callable function, but in here we just pass None, since the actual values will be delivered to our model on a later stage. The second argument is the number of dimensions. Since in our pricing function we only change the spot price and all the other variables are being fixed, our model is one-dimensional. The third argument is constructed MocaxDomain object, which sets the domain for our model. In the fourth argument, we can set our error threshold, but in here we just pass None. The fifth argument is constructed MocaxNs object, which sets the accuracy for our model.

n_dimension = 1
n_chebyshev_points = 25
domain = mocaxpy.MocaxDomain([[lowest_spot, highest_spot]])
accuracy = mocaxpy.MocaxNs([n_chebyshev_points])
mocax = mocaxpy.Mocax(None, n_dimension, domain, None, accuracy)

At it's current state, our constructed (but still incomplete) Mocax object is only aware of dimensionality, domain and grid of Chebyshev points. The next step is to set the actual function values for each point in our Chebyshev grid. 

chebyshev_points = mocax.get_evaluation_points()
option_values_at_evaluation_points = [call_option(point[0], 100.0, 1.0, 0.25, 0.01) for point in chebyshev_points]
mocax.set_original_function_values(option_values_at_evaluation_points)
call_options_approximations = [mocax.eval([spot], derivativeId=0) for spot in spots]

First, we request back the information on Chebyshev grid points (total of 25 points) from Mocax object. We need to calculate function values for all these points, since we did not give any callable pricing function in our constructor. Next, we ask revaluations from the original pricing function for all Chebyshev grid points (total of 25 revaluations). Then, we handle these calculated values back to Mocax object. Finally, we request call option values from Mocax object. As a response, we will get one million values back from Mocax object: 25 of those values were being explicitly calculated by using original pricing function and the rest are being interpolated by Mocax object.

The complete example program for this section can be found in my GitHub page.

Example: 2-dimensional MoCaX approximation on valuing European call options

Again, let us value a portfolio of European call options, but this time by changing two variables: spot price and time to maturity. Spot price varies between 50 and 150 and time to maturity varies between 0.25 and 2.5. By dividing the both domains into one thousand steps, we get grid containing one million points and for full revaluation we get total of one million calls to our pricing function. As a result, we get the familiar 3D surface.

Processing time is about 330 seconds (5.5 minutes) to complete all calculations. 

Next, we calculate the approximations for option values by using Mocax object and 25 Chebyshev points for the both domains. Revaluation calls are being sent for 625 options and the rest will be interpolated by Mocax object. Processing time is about 13.7 seconds to complete all calculation. So, with just 625 Chebyshev points in our grid, we get remarkably close to the original pricing function values just with the fraction of original processing time. Error surface is shown below (maximum error is around 7.7e-08).

 

The complete example program for this section can be found in my GitHub page.

Further material

The main source for all information is MoCaX Intelligence company page and their collection of high-quality YouTube videos. 

The book "Machine Learning for Risk Calculations: A Practitioner's View" written by Ignacio Ruiz and Mariano Zeron is also available for sale.

QuantsHub YouTube channel is also containing 1-hour video on MoCaX, as presented by Ignacio Ruiz. Concerning the material presented in this post, the most essential videos to get started on using MoCaX as presented by Mariano Zeron can be found in here and in here.

The actual MoCaX library (C++ and Python) can be downloaded from software page. The downloaded package is professionally equipped with MoCaX API documentation (doxygen), as well as with program examples and PDF documentations explaining installation and the main usage of MoCaX API. 

Thanks for reading this blog.

-Mike