Where u and w are still undefined functions of r and t. This SDE must be solved either analytically (if such solution exists) or numerically (Monte Carlo, FDM). After solving the model, it can then be used to price different interest rate products.
The problem in these models lies in the model parameters (u, w). We could estimate those parameters from the set of market data, but in this case we (most probably) end up with a set of resulting theoretical bond prices, not matching with the corresponding market bond prices. In the case of valuing or hedging interest rate products, such prices would be then more or less useless. The second approach is to turn the whole scheme upside down. Instead of estimating parameters from the set of market data directly and then feeding those into model, we would solve a set of parameters in such a way, that our resulting theoretical bond prices will match exactly with the corresponding market bond prices. In this posting, we will solve that set of parameters numerically.
Just for a reference, full derivation of Bond Pricing Equation (BPE), plus some solutions for tractable short rate models are presented in the book written by Paul Wilmott, for example.
PROJECT OUTCOME
The end product of this small project will be C# program, which will solve numerically time-dependent theta parameters for a given short rate model (Ho-Lee as our example case) for a given set of market zero-coupon bond prices, assuming that time-dependent theta parameters are piecewise constant. C# program is using Microsoft Solver Foundation for performing the required optimization tasks. Finally, we will interface C# program into Excel workbook via VBA, with Excel-DNA.ANALYTICAL SOLUTION FOR HO-LEE SHORT RATE MODEL
Ho-Lee model was the first no-arbitrage-type short rate model, which could be calibrated to market data. In this first section, we will go through the process of solving this SDE analytically. SDE for Ho-Lee model is the following.
Where theta is time-dependent drift coefficient (u), sigma is constant diffusion coefficient (w) and dx is the standard brownian motion. By replacing these coefficients into bond pricing equation (BPE), we get the following partial differential equation (PDE).
For this PDE, we are (very fortunately) looking for very specific solution, having the following functional form.
To solve our PDE above, we will substitute the previous solution into PDE. First, we calculate the following partial derivatives. Theta (in this case, partial derivative to time) is the following.
Delta is the following.
Gamma is the following.
.png)
After separating all r-dependent terms and r-independent terms, we will have two ordinary differential equations (ODE) to be solved. For B coefficient, ODE is the following.
For A coefficient, ODE is the following.
After integrating ODE for B coefficient from t to T, we have the following solution.
After integrating ODE for A coefficient from t to T and substituting B coefficient into equation, we have the following solution.
We could still continue and find the exact analytical solution for time-dependent theta coefficient from this integral equation. However, for any real-life calibration purposes we have to make some assumptions concerning theta parameter. For the sake of easiness in calculations, we assume this time-dependent theta parameter to be piecewise constant. With this assumption, we get the following solution for A coefficient.
After integrating the last existing integral term, we have the following solution for A coefficient.
Finally, we have the following functional form for a zero-coupon bond price according to Ho-Lee, which can be used for calibration purposes.
From this equation, we could also solve for the unknown theta parameter analytically, without any numerical methods involved.
CALIBRATION
The pricing process with models usually starts with some already known parameters, which are then feeded into some model to calculate the results. For example, in the case of Ho-Lee model, we would know the values for spot rate, time-dependent theta, constant sigma and bond maturity. Then, by calculating coefficients A and B we would calculate zero-coupon bond price and the corresponding yield.Concerning short rate models, these parameters are usually not known in advance and have to be estimated or calibrated. In the calibration process, we are performing the whole pricing process backwards. First, we know the market yield for a zero-coupon bond. From this yield we calculate the corresponding bond price. Assuming that we know (or have been estimating) the values for spot rate, maturity and constant sigma parameter, we can then solve for coefficient A and B. Finally, we can calculate the value for time-dependent theta parameter.
Consider the case, in which we have Libor zero curve as our input market data, consisting of N zero-coupon bond yields. From this curve, we calculate the corresponding N zero-coupon bond prices. Consider also, that we have statistically estimated the value for constant sigma (standard deviation of a short rate) and we know spot rate and N maturities. After this, we set N initial values for our piecewise constant theta parameters. By using these theta parameters, we then calculate N pairs of A and B coefficients. Finally, N theoretical bond prices and N theoretical yields can be calculated by using N pairs of A and B coefficients. In the final stage, we just adjust our initial values for our N piecewise constant theta parameters, until theoretical yields and corresponding market yields are equal for all N bonds. More specifically, we minimize the sum of absolute squared errors between theoretical yields and corresponding market yields. This part is just unconstrained minimization problem. As a result of this minimization we will solve N theta parameters, for which theoretical bond prices are matching exactly with market bond prices. In other words, we are calibrating our model to market data.
As already noted above, we are dealing with the model having analytical solution (affine or tractable models). In this case, there is actually no need for any numerical method when calibrating model parameters to market. However, for the sake of curiosity and craftmanship, we will perform this calibration process numerically.
PREPARATORY TASKS
Next, we have to get the tools for performing optimization needed in the calibration process. As a proud holder of the NAG licence, I would use these numerical libraries for the task. However, in this project we will use Microsoft Solver Foundation, since it is freely available without any costs involved. Next, download Solver Foundation solver (32-bit). If this package is completely alien for you, there are excellent hands-on tutorials available, written by Mathias Brandewinder in here and in here. Replicating and studying these examples will get you started with Solver Foundation.Also, download and unzip Excel-DNA Version 0.30 zip file to be ready when needed. This is the version I have been using so far, but I assume you can also use newer version 0.32. Concerning the tools needed, we are now ready to move on to create the actual C# program.
PROGRAM DESIGN
Design for C# program has been presented in the following UML chart. In order to understand better what is happening between the objects, some comments are given inside the blue boxes. The main point in this design is its flexibility to handle new one-factor models. This example has been specifically made using Ho-Lee model. However, user is able to create new implementations for CIR or Vasicek model, if needed.C# PROGRAM
Create a new C# Class project "SolverApp_25092014". Target framework is .NET Framework 4. Remember also to create a new reference into SolverFoundation dll file (Project - Add reference - Browse - \Microsoft.Solver.Foundation.dll). My dll file is found within the following folder: C:\Program Files (x86)\Reference Assemblies\Microsoft\Framework\.NETFramework\v4.0\Microsoft.Solver.Foundation.dll. The workhorse classes for this program are presented below. Create new class files and copyPaste the following codes into separate classes.using System; using System.Collections.Generic; using System.Linq; using System.Text; using Microsoft.SolverFoundation.Services; namespace SolverApp_25092014 { public interface IOneFactorModel { Term price(Term parameter, Term t); } }
using System; using System.Collections.Generic; using System.Linq; using System.Text; using Microsoft.SolverFoundation.Services; namespace SolverApp_25092014 { public abstract class OneFactorModel : IOneFactorModel { public abstract Term price(Term parameter, Term t); } }
using System; using System.Collections.Generic; using System.Linq; using System.Text; using Microsoft.SolverFoundation.Services; namespace SolverApp_25092014 { public class HoLee : OneFactorModel { private Term spot; private Term stdev; // public HoLee(double spot, double stdev) { this.stdev = stdev; this.spot = spot; } public override Term price(Term parameter, Term t) { // create term object for Ho-Lee bond price for a given eta and t Term B = t; Term c1 = Model.Quotient(1, 2); Term c2 = Model.Quotient(1, 6); Term A = -(parameter * (c1 * Model.Power(t, 2))) + c2 * Model.Power(stdev, 2) * Model.Power(t, 3); return Model.Exp(A - spot * B); } } }
using System; using System.Collections.Generic; using System.Linq; using System.Text; using Microsoft.SolverFoundation.Services; namespace SolverApp_25092014 { public class OneFactorCalibrator { private OneFactorModel model; private Dictionary<double, double> curve; // public OneFactorCalibrator(OneFactorModel model, Dictionary<double, double> curve) { this.model = model; this.curve = curve; } public List<double> calibrate() { // create a new solver model SolverContext solver = new SolverContext(); solver.ClearModel(); Model solverModel = solver.CreateModel(); // // create decision variables, a set of parameters to be calibrated var decisions = curve.Select(it => new Decision(Domain.Real, "parameter_" + it.Key.ToString())); solverModel.AddDecisions(decisions.ToArray()); // // create objective function as sum of differences between market and theoretical yields SumTermBuilder terms = new SumTermBuilder(curve.Count); int i = 0; foreach (KeyValuePair<double, double> kvp in curve) { // define required term objects Term eta = solverModel.Decisions.ElementAt(i++); Term t = kvp.Key; // // calculate bond prices and yields Term theoreticalPrice = model.price(eta, t); Term theoreticalYield = Model.Power(Model.Quotient(1, theoreticalPrice), Model.Quotient(1, t)) - 1; Term marketPrice = kvp.Value; Term marketYield = Model.Power(Model.Quotient(1, marketPrice), Model.Quotient(1, t)) - 1; Term yieldDifference = Model.Power(marketYield - theoreticalYield, 2); // // add constructed term into sumbuilder (objective function) terms.Add(yieldDifference); } // // define optimization goal, solve the model and pack results into list solverModel.AddGoal("solverGoal", GoalKind.Minimize, Model.Abs(terms.ToTerm())); Solution result = solver.Solve(); return solverModel.Decisions.Select(it => it.ToDouble()).ToList(); } } }
At this point, we should be able to build this class project without any errors or warnings. The only thing that might create a bit of confusion here, is the logic of using Solver Foundation and especially its Term object. If you feel uncomfortable using solver objects, you may spend some quality time and go through examples by Mathias Brandewinder mentioned earlier. Also, going through the stuff presented in Microsoft.Solverfoundation.Services Namespace relieves the painful climbing on this new learning curve. There are also some documentation pdf files included in the downloaded package from Microsoft. Anyway, the basic functionality for calibration process has now been set. Next, we have to interface our C# program and Excel.
Excel-DNA
Concerning the usage and creating interface between Excel and C#, we are following instructions presented in this blog posting.Add reference to Excel-DNA library (Project - Add reference - Browse - \\ExcelDna.Integration.dll) and click OK. This dll file is inside the distribution folder what we just downloaded from Excel-DNA website. From the properties of this reference, set Copy Local to be False.
Add new file as text file to project (Project - Add new item - Text file) and name it to be SolverApp_25092014.dna. CopyPaste the following xml code into this file.
<DnaLibrary Name="SolverApp_25092014" RuntimeVersion="v4.0"> <ExternalLibrary Path="SolverApp_25092014.dll" /> </DnaLibrary>
From the properties of this dna file, set Copy to Output Directory to be Copy if newer.
Next, from the downloaded Excel-DNA folder (Distribution), copy ExcelDna.xll file into your project folder (\\Projects\SolverApp_25092014\SolverApp_25092014) and rename it to be SolverApp_25092014.xll. Then, add this xll file into your current project (Project - Add existing item). At this point, it might be that you do not see anything else, except cs files on this window. From drop down box on the bottom right corner of this window, select All files and you should see ExcelInterface.xll file what we just pasted into this ExcelInterface folder. Select this file and press Add. Finally, from the properties of this xll file, set Copy to Output Directory to be Copy if newer.
Build the solution. Again, everything should have gone well without any errors or warnings. At this point, my \\SolverApp_25092014\bin\Release folder looks like the following.
EXCEL USER INTERFACE AND C#-VBA INTEGRATION
Add new class into project and name it to be "SolverApp_25092014". Remember also, that we might need to use Message Box for error reporting coming from catch block. Hence, we need to create reference to System.Windows.Forms library (Project - Add reference - .NET - System.Windows.Forms). CopyPaste the following code into this new class file. After this, build solution again and save it. We should be able to rebuild this class project again without any errors or warnings.using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Windows.Forms; using ExcelDna.Integration; namespace SolverApp_25092014 { public static class SolverApp_25092014 { public static void calibrate() { try { // create Excel application object dynamic Excel = ExcelDnaUtil.Application; // // read scalar parameters from named ranges double r = (double)Excel.Range["_r"].Value2; double stdev = (double)Excel.Range["_stdev"].Value2; // // read curve from named range dynamic Matrix = Excel.Range["_curve"].Value2; int rows = Matrix.GetUpperBound(0); // // export curve data into dictionary Dictionary<double, double> curve = new Dictionary<double, double>(); for (int i = 0; i < rows; i++) { double key = (double)Matrix.GetValue(i + 1, 1); double value = (double)Matrix.GetValue(i + 1, 2); curve.Add(key, value); } // // create model and calibrator instances OneFactorModel model = new HoLee(r, stdev); OneFactorCalibrator calibrator = new OneFactorCalibrator(model, curve); List<double> theta = calibrator.calibrate(); // // export theta parameters into 2-dimensional array double[,] result = new double[rows, 1]; for (int i = 0; i < theta.Count; i++) result[i, 0] = theta[i]; // // print array into named range Excel.Range["_theta"] = result; } catch (Exception e) { MessageBox.Show(e.Message.ToString()); } } } }
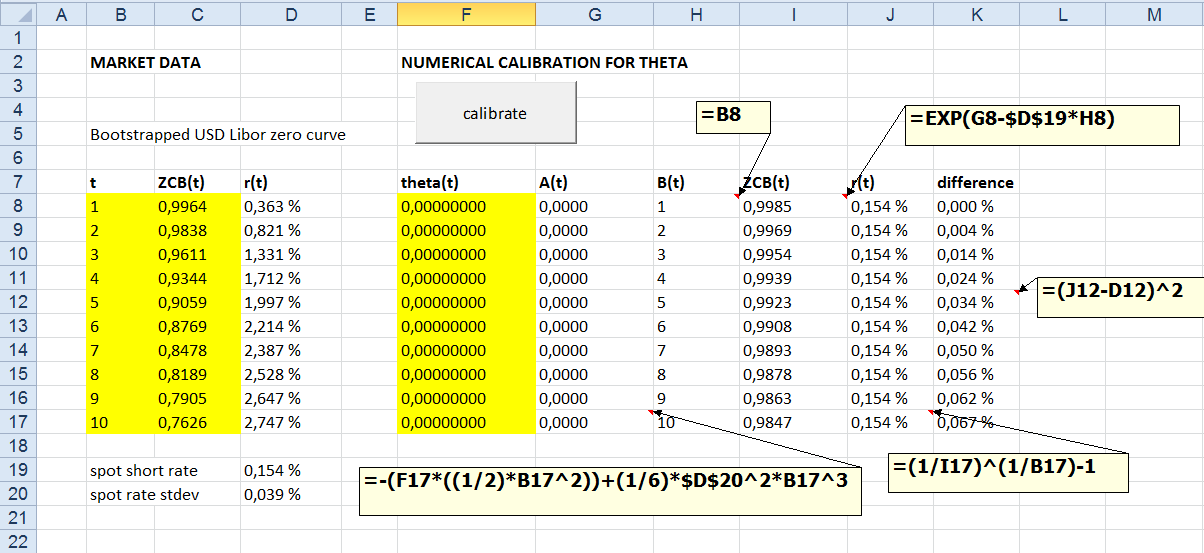
We are almost there. Next, we will create Excel worksheet interface and VBA "trigger program" for C# program. The action starts as the user is pressing commandbutton, which then calls a simple VBA program, which then triggers the actual C# workhorse program. Create the following data view into a new Excel worksheet. Also, insert command button into worksheet.
A few words concerning this worksheet. Zero-coupon bond curve maturities and prices are given in the columns B and C (yellow). Corresponding yields are calculated in the column D. Vector of time-dependent piecewise constant thetas will be calibrated and printed into column F (yellow). Columns from G to K are using analytical solution for Ho-Lee model to calculate theoretical zero-coupon bond prices and yields. Squared differences between market yields and calculated theoretical yields are given in the column K.
Input (output) data for (from) C# program are going to be read (written) directly from (to) Excel named ranges. Create the following named Excel ranges.
Finally, insert a new standard VBA module and create simple program calling the actual C# program (Sub tester). Also, create event-handling program for commandbutton click, which then calls the procedure shown below.
Concerning the program and its interfacing with Excel, all those small pieces have finally been assembled together. Now, it is time to do the actual calibration test run.
TEST RUN AND MODEL VALIDATION
In this section we will perform test run and check, whether our calibration model is working properly. In another words, are we able to replicate the market with our model. After pressing "calibrate" button, my Excel shows the following calibration results for theta parameters shown in column F.Analytical results are already calculated in the worksheet (columns G to J). For example, time-dependent theta parameter for 4 years is 0.00771677. With this theta value embedded in A coefficient will produce zero-coupon bond price, equal to corresponding market price.
How about using SDE directly with these calibrated time-dependent thetas? Let us use Monte Carlo to price 4-year zero-coupon bond by using SDE directly. For the sake of simplicity, we perform this exercise in Excel. Simulation scheme is presented in the screenshot below.
In this Excel worksheet presented above, 4-year period has been divided into 800 time steps, which gives us the size for one time step to be 0.005 years. Total of 16 378 paths was simulated by using Ho-Lee SDE with calibrated time-dependent piecewise constant theta parameter. All simulated zero-coupon bond prices have been calculated in the row 805. By taking the average for all these 16 378 simulated zero-coupon bond prices, gives us the value of 0.9343. Needless to say this value is random variable, which changes every time we press that F9 button. Our corresponding market price for 4-year zero-coupon bond is 0.9344, so we are not far away from that value. We can make the conclusion, that our calibration is working as expected.
Thanks for reading this blog.
-Mike

.png)

.png)
.png)

.png)
.png)

.png)
.png)
.png)
.png)